Числовые последовательности
Числовой последовательностью называется числовая функция, заданная на множестве натуральных чисел или на множестве  первых натуральных чисел. первых натуральных чисел.
Для числовых последовательностей вместо 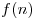 обычно пишут обычно пишут 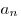 , саму последовательность обозначают , саму последовательность обозначают 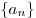 , общий член последовательности обозначают , общий член последовательности обозначают 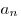 . Числа . Числа 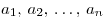 называются членами последовательности: называются членами последовательности: 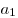 — первый член последовательности, — первый член последовательности, 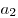 — второй член последовательности, — второй член последовательности, 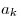 — — 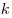 -ый член последовательности и т.д. -ый член последовательности и т.д.
Числовая последовательность определена, если указан закон, по которому каждому натуральному числу  ставиться в соответствие действительное число ставиться в соответствие действительное число 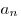 . .
Числовая последовательность может быть определена заданием ее  -го члена формулой, позволяющей найти любой член последовательности простой подстановкой номера искомого члена в эту формулу. Такой способ задания последовательности называется явным. -го члена формулой, позволяющей найти любой член последовательности простой подстановкой номера искомого члена в эту формулу. Такой способ задания последовательности называется явным.
Закон образования числовой последовательности может состоять в задании нескольких первых членов последовательности и рекуррентной формулы, с помощью которой каждый следующий член выражается через предыдущий (или несколько предыдущих). Такой способ задания последовательности называется рекуррентным.
Числовая последовательность называется возрастающей, если в ней каждый следующий член больше предыдущего.
Числовая последовательность называется убывающей, если в ней каждый следующий член меньше предыдущего.
Числовая последовательность называется ограниченной, если существует такое натуральное число 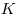 , что , что 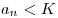 для любого натурального для любого натурального  . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
