Иррациональные неравенства
Иррациональными называются неравенства, в которых переменная содержится под знаком корня.
Иррациональное неравенство, как правило, сводится к равносильной системе (или совокупности систем) неравенств.
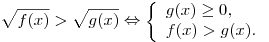
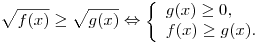
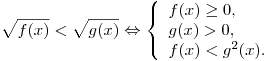
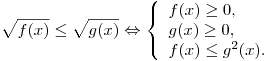
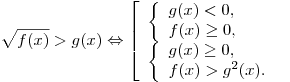
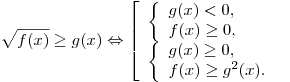
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
