Метод интервалов

Методом интервалов (иногда его называют также методом промежутков), называется метод решения неравенств, основанный на исследовании смены знаков функции. Данный метод находит применение в широком круге задач, в частности, при решении линейных неравенств, квадратных неравенств, дробно-линейных неравенств.

В основе метода интервалов лежат следующие положения:

1. Знак произведения (частного) однозначно определяется знаками сомножителей (делимого и делителя).
2. Знак произведения не изменится (изменится на противоположный), если изменить знак у четного (нечетного) числа сомножителей.
3. Знак многочлена справа от большего (или единственного) корня совпадает со знаком его старшего коэффициента. В случае отсутствия корней знак многочлена совпадает со знаком его старшего коэффициента на всей области определения.
4. Если строго возрастающая (убывающая) функция имеет корень, то справа от корня она положительна (отрицательна) и при переходе через корень меняет знак.

Рассмотрим основную схему решения неравенства вида 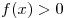(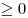, , 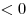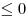) методом интервалов.

1. Найти область определения функции .
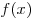2. Найти нули функции .
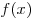3. На числовую прямую нанести область определения и нули функции. Нули функции разбивают ее область определения на промежутки, в каждом из которых функция сохраняет постоянный знак.
4. Найти знаки функции в полученных промежутках, вычислив значение функции в какой-либо одной точке из каждого промежутка.
5. Записать ответ.