Квадратные неравенства
Квадратным неравенством называется неравенство 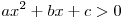 или или 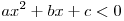 (возможны также нестрогие неравенства). (возможны также нестрогие неравенства).
Решение неравенств вида 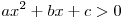 (остальные решаются аналогично). (остальные решаются аналогично).
Пусть 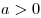 , , 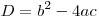 — дискриминант квадратного трехчлена — дискриминант квадратного трехчлена 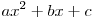 , , 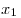 и и 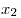 — его действительные корни. — его действительные корни.
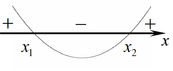
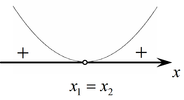
- При
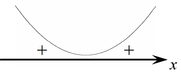
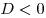 : квадратный трехчлен в левой части имеет знак старшего коэффициента, т.е. при : квадратный трехчлен в левой части имеет знак старшего коэффициента, т.е. при 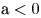 решений нет, а при решений нет, а при 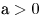 , , 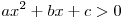 при всех действительных значениях при всех действительных значениях  . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
