Иррациональные уравнения
Иррациональными называются уравнения, в которых переменная содержится под знаком корня.
Иррациональное уравнение, как правило, сводится к равносильной системе, содержащей уравнения и неравенства.
Равносильность уравнений, содержащих неизвестное под знаком корня
1. Уравнение
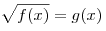
равносильно системе
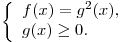
2. Уравнение
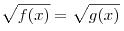
равносильно любой из систем:
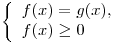 или или 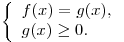
Примечание. Если функция  возрастает на множестве возрастает на множестве  , а функция , а функция 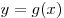 убывает на множестве убывает на множестве  , то уравнение , то уравнение 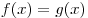 имеет на имеет на  не более одного корня. не более одного корня.
Иррациональные уравнения могут быть также решены путем возведения обеих частей уравнения в натуральную степень. При возведении уравнения в степень могут появится посторонние корни. Поэтому необходимой частью данного метода решения иррационального уравнения является проверка.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
