Квадратные уравнения
Квадратное уравнение — уравнение вида 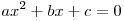 ( (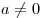 ), где ), где 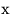 — неизвестное, — неизвестное, 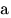 , ,  , ,  — вещественные числа. — вещественные числа.
Дискриминант квадратного уравнения вычисляется следующим образом:
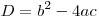 . .
Если 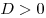 , уравнение имеет 2 корня. Если , уравнение имеет 2 корня. Если 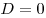 , уравнение имеет один корень. Если , уравнение имеет один корень. Если 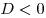 , уравнение не имеет вещественных корней. , уравнение не имеет вещественных корней.
Корни данного уравнения находятся по формуле:
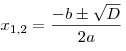 . .
Уравнение вида 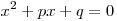 называется приведенным квадратным уравнением. Корни данного уравнения находятся по формуле: называется приведенным квадратным уравнением. Корни данного уравнения находятся по формуле:
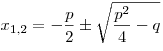 . .
Для квадратного уравнения вида 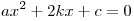 ( (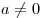 ) корни могут быть найдены по формуле: ) корни могут быть найдены по формуле:
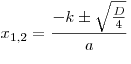 . .
Теорема Виета для квадратных уравнений
Теорема Виета. Если уравнение 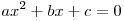 ( (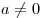 ) имеет 2 корня, то их сумма равна ) имеет 2 корня, то их сумма равна 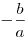 , а произведение равно , а произведение равно 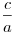 . .
Биквадратные уравнения
Биквадратным называется уравнение вида 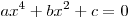 , где , где 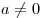 . .
Биквадратное уравнение решается методом введения новой переменной: положив 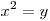 , прийдем к квадратному уравнению , прийдем к квадратному уравнению 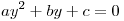 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
