Степень с действительным показателем
Пусть дано положительное число  и произвольное действительное число и произвольное действительное число  . Число . Число 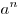 называется степенью, число называется степенью, число  — основанием степени, число — основанием степени, число  — показателем степени. — показателем степени.
По определению полагают:
Если  и и  — положительные числа, — положительные числа,  и и 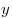 — любые действительные числа, то справедливы следующие свойства: — любые действительные числа, то справедливы следующие свойства:
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
