Степень с рациональным показателем
Пусть дано положительное число  и произвольное рациональное число и произвольное рациональное число  . Число . Число 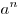 называется степенью, число называется степенью, число  — основанием степени, число — основанием степени, число  — показателем степени. — показателем степени.
По определению полагают:
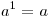 . .
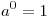 . .
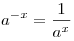 , , 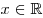 . .
- Если
 — целое, а — целое, а  — натуральное число и — натуральное число и 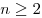 , то , то ![a^{\frac{m}{n}} = \sqrt[n]{{a^m }} a^{\frac{m}{n}} = \sqrt[n]{{a^m }}](/inc/pictures/9a473c829f075bdc5fef017b92658ada.png) . .
Частные случаи:
Свойства степени с рациональным показателем
Если  и и  — положительные числа, — положительные числа,  и и 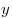 — любые рациональные числа, то справедливы следующие свойства: — любые рациональные числа, то справедливы следующие свойства:
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
