Корень n-ной степени
Пусть  — натуральное число, неравное единице. Если — натуральное число, неравное единице. Если  — четно, то арифметическим корнем — четно, то арифметическим корнем  -ной степени из неотрицательного числа -ной степени из неотрицательного числа  называется такое неотрицательное число, называется такое неотрицательное число,  -ная степень которого равна -ная степень которого равна  . Если . Если  — нечетно, то арифметическим корнем — нечетно, то арифметическим корнем  -ной степени из числа -ной степени из числа  называется такое число, называется такое число,  -ная степень которого равна -ная степень которого равна  . .
По определению:
![(\sqrt[n]{a})^n = a (\sqrt[n]{a})^n = a](/inc/pictures/0c64b3d22b377683aed4bde2b0c8e1d2.png) . .
Если  и и  — неотрицательные числа, — неотрицательные числа,  и и 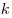 — натуральные числа, отличные от единицы, — натуральные числа, отличные от единицы,  — целое число, то имеют место следующие соотношения: — целое число, то имеют место следующие соотношения:
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
