Логарифм
Логарифмом положительного числа  по основанию по основанию  ( (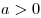 , , 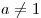 ) называют показатель степени, в которую нужно возвести число ) называют показатель степени, в которую нужно возвести число  , чтобы получить число , чтобы получить число  . .
Для логарифма положительного числа  по основанию по основанию  ( (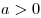 , , 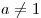 ) используется обозначение ) используется обозначение 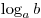 . .
По определению: 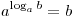 , это равенство называется основным логарифмическим тождеством. , это равенство называется основным логарифмическим тождеством.
Частные случаи:
Логарифм положительного числа  по основанию по основанию 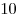 называется десятичным логарифмом и обозначается называется десятичным логарифмом и обозначается 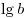 . .
Числом 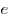 называется бесконечная сумма называется бесконечная сумма
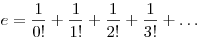 . .
Число 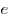 приблизительно равно приблизительно равно 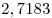 . .
Логарифм положительного числа  по основанию по основанию 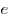 называется натуральным логарифмом и обозначается называется натуральным логарифмом и обозначается 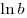 . .
Свойства логарифмов
Если 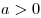 , , 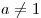 , , 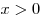 , , 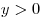 , , 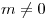 , ,  — любое действительное число, то справедливы следующие свойства: — любое действительное число, то справедливы следующие свойства:
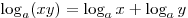 ; ;
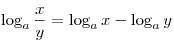 ; ;
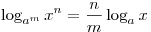 ; ;
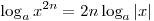 , , 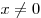 , , 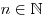 ; ;
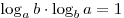 , , 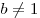 ; ;
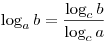 , где , где 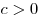 , , 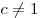 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
