Многочлены от одной переменной
Выражение вида 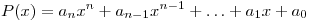 , где , где 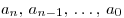 — некоторые числа и — некоторые числа и 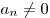 , называется многочленом степени , называется многочленом степени  от от  . .
Два многочлена называются тождественно равными, если их числовые значения совпадают при всех значениях  . Многочлены . Многочлены 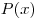 и и 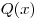 тождественно равны тогда и только тогда, когда они совпадают, т.е. коэффициенты при одинаковых степенях тождественно равны тогда и только тогда, когда они совпадают, т.е. коэффициенты при одинаковых степенях  этих многочленов одинаковы. этих многочленов одинаковы.
При делении многочлена 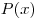 на многочлен на многочлен 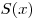 (например «уголком») получаем многочлен (например «уголком») получаем многочлен 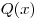 (неполное частное) и остаток — многочлен (неполное частное) и остаток — многочлен 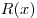 (в случае, когда остаток (в случае, когда остаток 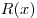 равен нулю, многочлен равен нулю, многочлен 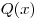 называется частным). Если называется частным). Если 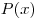 — делимое, — делимое, 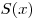 — делитель, то многочлен — делитель, то многочлен 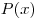 представим в виде представим в виде 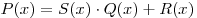 . При этом сумма степеней многочленов . При этом сумма степеней многочленов 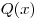 и и 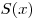 равна степени многочлена равна степени многочлена 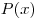 , а степень остатка , а степень остатка 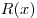 меньше степени делителя меньше степени делителя 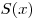 . .
Схема Горнера
(схема деления многочлена 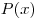 на двучлен на двучлен  ) )
Пусть 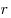 — остаток от деления многочлена — остаток от деления многочлена 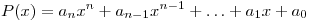 на двучлен на двучлен  и и 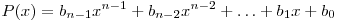 — частное. — частное.
Тогда, имеет место следующее правило для определения коэффициентов 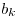 и остатка и остатка 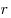 : :
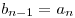 ; ; 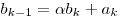 , ( , (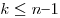 ); ); 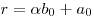 . .
Это правило удобно переписать в виде следующей таблицы (схемы Горнера):
Теорема Безу
Теорема Безу. Остаток от деления многочлена 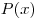 на двучлен на двучлен  равен значению этого многочлена при равен значению этого многочлена при 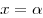 . .
Следствие 1:
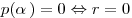 . .
Таким образом, число 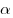 является корнем многочлена является корнем многочлена 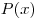 тогда и только тогда, когда многочлен тогда и только тогда, когда многочлен 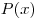 делится на двучлен делится на двучлен  без остатка. без остатка.
Если многочлен 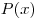 делится без остатка на делится без остатка на 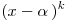 , но не делится без остатка на , но не делится без остатка на 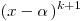 , то число , то число 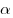 называется корнем кратности называется корнем кратности 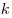 для многочлена для многочлена 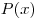 . .
Следствие 1. Многочлен 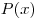 степени степени  имеет не более имеет не более  корней. корней.
Следствие 2. Если многочлен 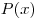 степени степени  имеет имеет  корней (среди которых могут быть равные), то он представим в виде: корней (среди которых могут быть равные), то он представим в виде:
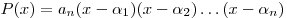 . .
Теорема Виета
Теорема Виета. Если многочлен 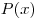 степени степени  имеет имеет  различных корней различных корней 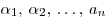 , то имеют место следующие соотношения: , то имеют место следующие соотношения:
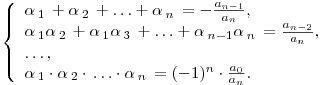
Замечание. Формулы Виета сохраняют силу и при наличии кратных корней, но в этом случае надо каждый корень учитывается столько раз, какова его кратность.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
