Многочлены. Основные понятия и формулы
Многочленом называют алгебраическую сумму одночленов, например: 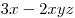 , , 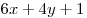 . Привести многочлен к стандартному виду — означает привести к стандартному виду все его члены, а затем привести подобные члены. . Привести многочлен к стандартному виду — означает привести к стандартному виду все его члены, а затем привести подобные члены.
При сложении и вычитании многочленов используются стандартные законы сложения и вычитания выражений.
Чтобы умножить многочлен на одночлен, надо умножить на этот одночлен все члены многочлена и полученное произведение сложить. После этого следует привести полученный многочлен к стандартному виду.
Формулы сокращенного умножения
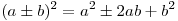 . .
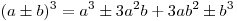 или
или 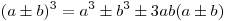 . .
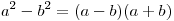 . .
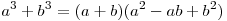 . .
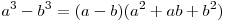 . .
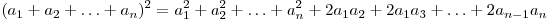 . .
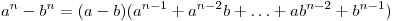 . .
Для возведения двучлена в любую натуральную степень служит следующая формула, называемая формулой бинома Ньютона:
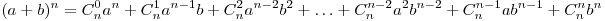 , ,
где 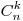 — элемент, стоящий на — элемент, стоящий на 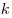 -м месте в -м месте в  -ной строчке треугольника Паскаля (см. ниже): -ной строчке треугольника Паскаля (см. ниже):
Числа, стоящие в каждой последующей строке треугольника Паскаля, получаются сложением соответствующих чисел предыдущей строки и являются коэффициентами разложения при данном  . При этом показатели степени числа . При этом показатели степени числа  убывают от убывают от  до до 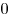 , а показатели степени числа , а показатели степени числа  возрастают от возрастают от 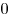 до до  . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
