Числовые неравенства
Определение 1. Число  называется большим (меньшим) числа называется большим (меньшим) числа  , если разность , если разность  положительна (отрицательна). положительна (отрицательна).
Из определения следует, что любое положительное число больше нуля, а любое отрицательное число меньше нуля, поэтому вместо слов
«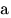 — положительное (отрицательное) число» часто употребляется запись « — положительное (отрицательное) число» часто употребляется запись «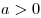 ( (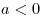 )». )».
Основные свойства числовых неравенств
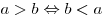 . .
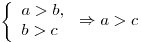 . .
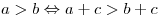 . .
- Если
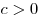 , то , то 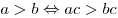 . .
- Если
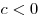 , то , то 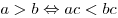 . .
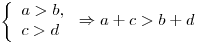 . .
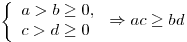 . .
- Если
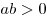 , то , то 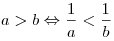 . .
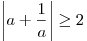 . .
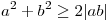 . .
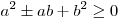 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
