Представление комплексных чисел
Алгебраическая форма
Запись комплексного числа 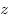 в виде в виде 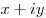 , , 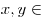  , называется алгебраической формой комплексного числа. , называется алгебраической формой комплексного числа.
Сумма и произведение комплексных чисел может быть вычислена непосредственным суммированием и перемножением таких выражений, с учетом тождества 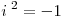 . .
Тригонометрическая и показательная формы
Если вещественную  и мнимую и мнимую 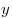 части комплексного числа выразить через модуль части комплексного числа выразить через модуль 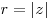 и аргумент и аргумент 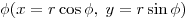 , то комплексное число , то комплексное число 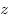 можно записать в тригонометрической форме: можно записать в тригонометрической форме:
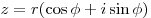 . .
Также может быть полезна следующая форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:
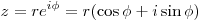 , ,
где 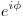 — расширение экспоненты для случая комплексного показателя степени. — расширение экспоненты для случая комплексного показателя степени.
Геометрическое представление
Если на плоскости по оси абсцисс расположить действительную часть, а по оси ординат — мнимую, то комплексному числу будет соответствовать точка с декартовыми координатами  и и 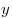 (или ее радиус-вектор, что то же самое), а модуль и аргумент будут полярными координатами этой точки. (или ее радиус-вектор, что то же самое), а модуль и аргумент будут полярными координатами этой точки.
В геометрическом представлении сумма комплексных чисел соответствует векторной сумме соответствующих векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Отсюда, в частности, получается Формула Муавра.
Формула Муавра
Формула, позволяющая возводить в степень комплексное число, представленное в тригонометрической форме:
![z^n = [r(\cos \phi + i\sin \phi)]^n = r^n (\cos n\phi + i\sin n\phi) z^n = [r(\cos \phi + i\sin \phi)]^n = r^n (\cos n\phi + i\sin n\phi)](/inc/pictures/e3c6f33ee55caeeae619746b4a597384.png) , ,
где 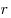 — модуль, а — модуль, а 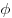 — аргумент комплексного числа. — аргумент комплексного числа.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
