Комплексные числа
Комплексное число 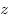 — это пара вещественных чисел — это пара вещественных чисел 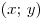 со введенными на них следующим образом операциями сложения и умножения: со введенными на них следующим образом операциями сложения и умножения:
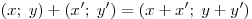 . .
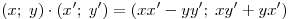 . .
Число 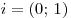 называется мнимой единицей. называется мнимой единицей.
Другая форма записи комплексного числа — 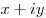 (что эквивалентно паре (что эквивалентно паре 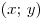 ). ).
Свойства операций над комплексными числами
- Сложение
 . .
- Вычитание
 . .
- Умножение
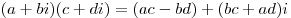 . .
- Деление
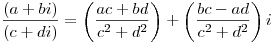 . .
Комплексные числа 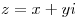 и и 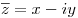 называются комплексно сопряженными. Для любых комплексных чисел верны равенства: называются комплексно сопряженными. Для любых комплексных чисел верны равенства:
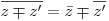 ; ; 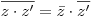 . .
Основные определения и обозначения
Комплексная переменная обычно обозначается 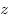 . Пусть . Пусть  и и 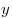 суть вещественные числа, такие, что суть вещественные числа, такие, что 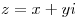 . Тогда: . Тогда:
- Числа
 и и 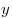 называются соответственно вещественной (Real) и мнимой (Imaginary) частями называются соответственно вещественной (Real) и мнимой (Imaginary) частями 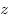 . Если . Если  , то , то 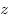 называется мнимым или чисто мнимым. называется мнимым или чисто мнимым.
- Число
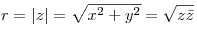 называется модулем числа называется модулем числа 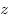 . .
- Угол
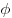 такой, что такой, что 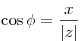 и и 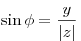 ,
называется аргументом ,
называется аргументом 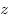 . .
Комплексное число 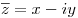 называется сопряженным (или комплексно сопряженным) к числу называется сопряженным (или комплексно сопряженным) к числу 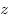 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
