Признаки делимости
- Число делится на 2 тогда и только тогда, когда последняя цифра делится
на 2 (то есть четная).
- Число делится на 3 тогда и только тогда, когда сумма цифр делится на 3
(так как все числа вида
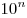 при делении на 3 дают в
остатке единицу). при делении на 3 дают в
остатке единицу).
- Число делится на 4 тогда и только тогда, когда двузначное число,
составленное из двух последних цифр, делится на 4.
- Число делится на 5 тогда и только тогда, когда последняя цифра делится
на 5 (то есть равна 0 или 5).
- Чтобы узнать, делится ли число на 7 (на 13), надо разбить его
десятичную запись справа налево на группы по 3 цифры в каждой (самая
левая группа может содержать 1 или 2 цифры), после чего взять группы с
нечетными номерами со знаком «минус», а с четными номерами — со знаком «плюс». Если полученное выражение делится на 7 (на 13), то и заданное число делится на 7 (на 13).
- Число делится на 8 тогда и только тогда, когда трехзначное число,
составленное из трех последних цифр, делится на 8.
- Число делится на 9 тогда и только тогда, когда сумма цифр делится на
9.
- Число делится на 10 тогда и только тогда, когда последняя цифра — ноль.
- Число делится на 11 тогда и только тогда, когда сумма его цифр,
стоящих на четных местах в десятичной записи, и сумма его цифр, стоящих
на нечетных местах в десятичной записи, дают одинаковые остатки при
делении на 11.
Утверждения, связанные с делимостью чисел
- Если
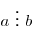 и и 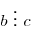 , то , то
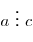 . .
- Если
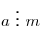 , то и , то и 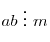 . .
- Если
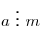 и и 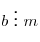 , то
и , то
и 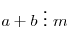 . .
- Если
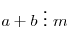 и и 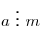 , то и , то и 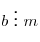
- Если
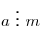 и и 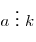 ,
причем ,
причем  и и 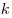 взаимно просты, то взаимно просты, то 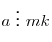 . .
- Если
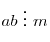 и и  взаимно просто с взаимно просто с
 , то , то 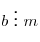 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

