Делимость натуральных чисел
Говорят, что натуральное число 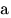 делится на
натуральное число делится на
натуральное число  , если существует такое натуральное число , если существует такое натуральное число
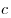 , что , что 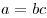 . При этом пишут: . При этом пишут: 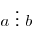 . В этом случае . В этом случае  называют делителем числа называют делителем числа
 , а , а  — кратным числа — кратным числа  . .
Число называется простым, если у него нет
делителей, отличных от него самого и от единицы (например: 2, 3, 5, 7 и т.
д.).
Число называется составным, если оно не является
простым.
Единица не является ни простым, ни составным.
Число  делится на простое число делится на простое число  в том и только в том случае, если
в том и только в том случае, если  встречается среди простых
множителей, на которые разлагается встречается среди простых
множителей, на которые разлагается  . .
Наибольшим общим делителем чисел 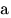 и и
 называется наибольшее число, одновременно являющееся
делителем называется наибольшее число, одновременно являющееся
делителем 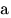 и делителем и делителем  (обозначается НОД (обозначается НОД
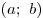 или или 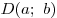 ). ).
Наименьшим общим кратным называют наименьшее число,
делящееся и на  , и на , и на  (обозначается НОК (обозначается НОК
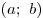 или или 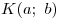 ). ).
Числа  и и  называют взаимно
простыми, если их наибольший общий делитель равен называют взаимно
простыми, если их наибольший общий делитель равен 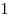 . .
Основная теорема арифметики
Всякое натуральное число  единственным
образом (с точностью до порядка множителей) раскладывается в произведение
степеней простых сомножителей: единственным
образом (с точностью до порядка множителей) раскладывается в произведение
степеней простых сомножителей:
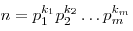 , ,
здесь  — простые
делители числа — простые
делители числа  , а , а  —
степени вхождения (степени кратности) этих делителей. —
степени вхождения (степени кратности) этих делителей.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
