Целые числа
Целые числа представляют собой множество 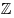 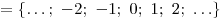 ,
состоящее из натуральных чисел, чисел, вида ,
состоящее из натуральных чисел, чисел, вида 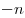
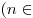 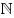 ) и числа нуль. ) и числа нуль.
Положительными целыми числами называют натуральные числа,
отрицательными — все остальные, кроме нуля.
Свойства операций над целыми числами
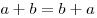 (коммутативность сложения). (коммутативность сложения).
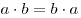 (коммутативность умножения). (коммутативность умножения).
 (ассоциативность сложения). (ассоциативность сложения).
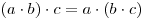 (ассоциативность умножения). (ассоциативность умножения).
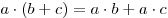 (дистрибутивность умножения относительно сложения). (дистрибутивность умножения относительно сложения).
Свойства целых чисел
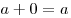 (существование нейтрального элемента). (существование нейтрального элемента).
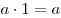 (существование нейтрального элемента). (существование нейтрального элемента).
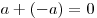 (существование противоположного элемента). (существование противоположного элемента).
Легко видеть, что операция деления может вывести нас за пределы множества. Например, 3 и 4 — целые числа, но их отношение уже не является целым числом.
На множестве целых чисел можно определить так называемое деление с остатком: для любых целых a и b, 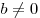 , существует единственный набор целых чисел q и r, что , существует единственный набор целых чисел q и r, что 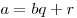 и и 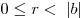 , где , где 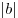 — абсолютная величина числа b. Здесь a — делимое, b — делитель, q — частное,
r — остаток. Если остаток от деления a на b
равен 0, то говорят, что число a делится на число b. — абсолютная величина числа b. Здесь a — делимое, b — делитель, q — частное,
r — остаток. Если остаток от деления a на b
равен 0, то говорят, что число a делится на число b.
Если  и и  — целые числа, но — целые числа, но  не является кратным не является кратным  , тогда говорят, что , тогда говорят, что  делится на
делится на  с остатком: с остатком: 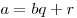 и и 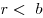 , где , где  — делимое, — делимое,  — делитель, — делитель, 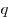 — частное. — частное.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
