Натуральные числа
Натуральные числа представляют собой множество 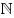 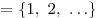 , снабженное естественным порядком. Существует бесконечное множество натуральных чисел — для любого натурального числа найдется другое натуральное число, большее его. , снабженное естественным порядком. Существует бесконечное множество натуральных чисел — для любого натурального числа найдется другое натуральное число, большее его.
Замкнутые операции над натуральными числами(операции, не выводящие результат из множества натуральных чисел)
К замкнутым операциям над натуральными числами относятся следующие арифметические операции:
- Операция сложения
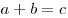 , где , где 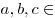 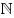 . .
- Операция умножения
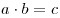 , где , где 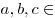 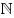 . .
- Возведение в степень
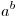 , где , где 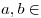 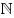 . .
Свойства операций над натуральными числами
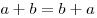 (коммутативность сложения). (коммутативность сложения).
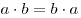 (коммутативность умножения). (коммутативность умножения).
 (ассоциативность сложения). (ассоциативность сложения).
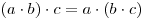 (ассоциативность умножения). (ассоциативность умножения).
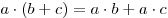 (дистрибутивность умножения относительно
сложения). (дистрибутивность умножения относительно
сложения).
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
