Параллелепипед

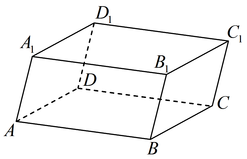
Параллелепипедом называется призма, основанием которой служит параллелограмм.

Параллелограммы, из которых составлен параллелепипед, называются его гранями, их стороны — ребрами, а вершины параллелограммов — вершинами параллелепипеда. У параллелепипеда все грани — параллелограммы.

Параллелепипеды, как и всякие призмы, могут быть прямые и наклонные.

Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, не принадлежащие основаниям, называют боковыми ребрами.

Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих ребер — противоположными.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда.

Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники.

Длины не параллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями). У прямоугольного параллелепипеда три линейных размера.