Векторы
Если 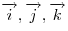 — попарно перпендикулярные единичные векторы, так
называемый ортонормированный базис, то любой вектор — попарно перпендикулярные единичные векторы, так
называемый ортонормированный базис, то любой вектор
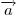 пространства может быть
единственным образом разложен по этим векторам, т.е. представлен в виде пространства может быть
единственным образом разложен по этим векторам, т.е. представлен в виде
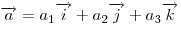 . .
Числа 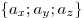 называются декартовыми
координатами вектора называются декартовыми
координатами вектора 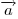 в базисе в базисе
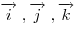 . Декартовые координаты вектора являются проекциями этого вектора
на соответствующие оси системы координат: . Декартовые координаты вектора являются проекциями этого вектора
на соответствующие оси системы координат:
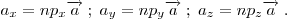
Если числа 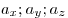 отличны от нуля, то отличны от нуля, то
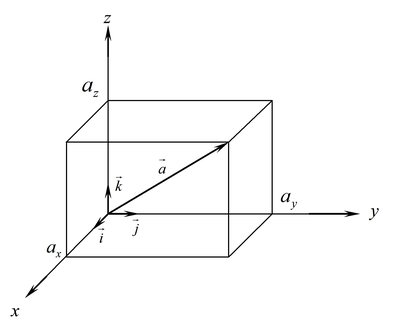
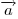 можно изобразить с помощью диагонали
прямоугольного параллелепипеда, у которого длины ребер равны можно изобразить с помощью диагонали
прямоугольного параллелепипеда, у которого длины ребер равны 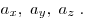
Если вектор 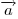 отложенный от точки отложенный от точки  с координатами
с координатами 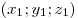 и кончаются в точке и кончаются в точке  с координатами
с координатами 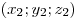 , то координаты вектора
определяются через координаты начала и конца вектора по формулам: , то координаты вектора
определяются через координаты начала и конца вектора по формулам:
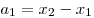
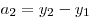
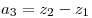
то есть:
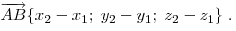
Если 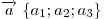 и и
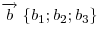 — два
произвольных вектора, то: — два
произвольных вектора, то:
Координаты суммы векторов равны сумме соответствующих координат
слагаемых
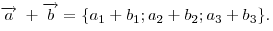 . .
Координаты разности векторов равны разности соответствующих координат
этих векторов
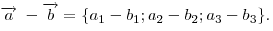
Координаты произведения на число 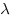 равны
произведению соответствующих координат векторов на данное число равны
произведению соответствующих координат векторов на данное число
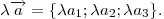
Линейная комбинация 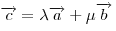 векторов векторов 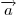 и и 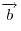 , где , где 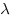 и и
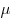 — произвольные числа, соответствуют координаты — произвольные числа, соответствуют координаты
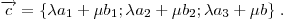
Скалярное произведение векторов определяется как
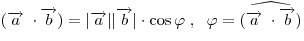
Величина скалярного произведения определяется через координаты
векторов по формуле
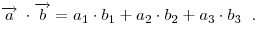
Длина вектора 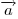 с координатами с координатами 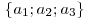 дается формулой дается формулой
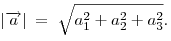
Угол между векторами 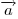 и и
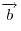 определяется из равенства определяется из равенства
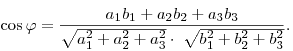
Всякое линейное уравнение
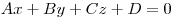
связывающие координаты 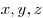 определяет множество точек
пространства, лежащих на плоскости, и, наоборот, каждую плоскость можно
задать линейным уравнением с тремя неизвестными, имеющих по крайне мере
один ненулевой коэффициент при переменных. определяет множество точек
пространства, лежащих на плоскости, и, наоборот, каждую плоскость можно
задать линейным уравнением с тремя неизвестными, имеющих по крайне мере
один ненулевой коэффициент при переменных.
Угол между двумя плоскостями 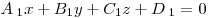 и и 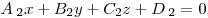 находится как угол между перпендикулярными векторами
находится как угол между перпендикулярными векторами
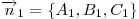 и и
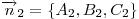 , т.е. по
формуле , т.е. по
формуле
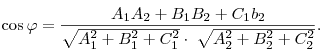
Расстояние 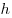 от точки от точки 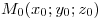 до
плоскости до
плоскости 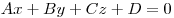 дается формулой дается формулой
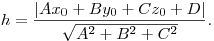
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
