Трехгранные углы
Объединение всех лучей, имеющих общее начало  , и пересекающих
данный треугольник , и пересекающих
данный треугольник  , называются трехгранным углом. , называются трехгранным углом.
Величина каждого плоского угла трехгранного угла меньше суммы величин
двух других его плоских углов:
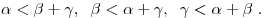
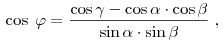
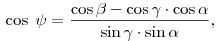
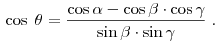
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
