Теоремы о перпендикулярности прямых и плоскостей
Для того что бы прямая  была перпендикулярна
плоскости была перпендикулярна
плоскости 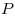 , необходимо и достаточно, чтобы она была
перпендикулярна двум произвольным непараллельным прямым , необходимо и достаточно, чтобы она была
перпендикулярна двум произвольным непараллельным прямым 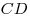 и
и 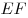 , лежащим в этой плоскости. , лежащим в этой плоскости.
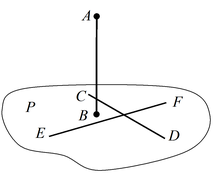
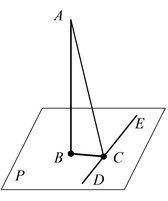
Для того, чтобы прямая 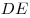 проведенная на плоскости проведенная на плоскости
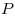 через основание наклонной через основание наклонной 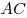 была ей перпендикулярна,
необходимо и достаточно, чтобы эта прямая была перпендикулярна к
проекции была ей перпендикулярна,
необходимо и достаточно, чтобы эта прямая была перпендикулярна к
проекции  , наклонной на плоскость , наклонной на плоскость 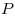 (Достаточное
условие этой теоремы называется «Теоремой о трех
перпендикулярах»: (Достаточное
условие этой теоремы называется «Теоремой о трех
перпендикулярах»: 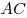 , ,  , , 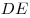 ). ).
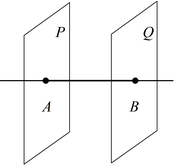
Если две прямые  и и 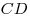 перпендикулярны
одной плоскости перпендикулярны
одной плоскости 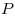 , то они параллельны между собой. , то они параллельны между собой.
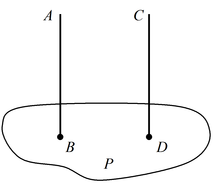
Если две плоскости 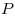 и и 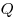 перпендикулярны
одной прямой перпендикулярны
одной прямой  , то они параллельны друг другу. , то они параллельны друг другу.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

