|
Системы счисления
Система счисления — символический метод записи чисел, представление чисел с помощью письменных знаков. Системы счисления подразделяются на позиционные, непозиционные и
смешанные.
Позиционные системы счисления
В позиционных системах счисления один и тот же числовой знак (цифра) в
записи числа имеет различные значения в зависимости от того места
(разряда), где он расположен. К числу таких систем относится
современная десятичная система счисления, возникновение которой связано
со счётом на пальцах.
Каждая позиционная система счисления определяется некоторым
натуральным числом 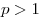 (основание системы
счисления) таким, что (основание системы
счисления) таким, что  единиц в каждом разряде
объединяется в одну единицу следующего по старшинству разряда. Система
счисления с основанием единиц в каждом разряде
объединяется в одну единицу следующего по старшинству разряда. Система
счисления с основанием  также называется также называется
 -ичной. -ичной.
Число  в в  -ичной системе счисления представляется в виде линейной комбинации степеней числа -ичной системе счисления представляется в виде линейной комбинации степеней числа  : :
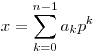 , ,
Где 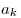 — это целые числа, называемые
цифрами, удовлетворяющие неравенству — это целые числа, называемые
цифрами, удовлетворяющие неравенству 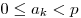 , ,
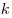 — порядковый номер разряда, начиная с
нулевого, — порядковый номер разряда, начиная с
нулевого,  — число разрядов. — число разрядов.
Каждая степень 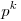 в такой записи называется
разрядом, старшинство разрядов и соответствующих им цифр
определяется значением показателя в такой записи называется
разрядом, старшинство разрядов и соответствующих им цифр
определяется значением показателя 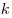 . Обычно для ненулевого
числа . Обычно для ненулевого
числа  требуют, чтобы старшая цифра требуют, чтобы старшая цифра 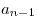 в в
 -ичном представлении -ичном представлении  была также ненулевой. была также ненулевой.
Если не возникает разночтений (например, когда все цифры
представляются в виде уникальных письменных знаков), число x
записывают в виде последовательности его  -ичных разрядных
единиц, перечисляемых по убыванию старшинства разрядов слева направо: -ичных разрядных
единиц, перечисляемых по убыванию старшинства разрядов слева направо:
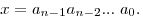
Наиболее употребительными в настоящее время позиционными системами
являются:
2 — двоичная (в дискретной математике, информатике,
программировании).
10 — десятичная система счисления (привычная нам система).
16 — шестнадцатеричная (наиболее часто используется в
программировании).
60 — шестидесятеричная (измерение углов и, в частности, долготы
и широты).
Смешанные системы счисления
Смешанная система счисления является обобщением
 -ичной системы счисления и также зачастую относится к
позиционным системам счисления. Основанием смешанной системы счисления
является возрастающая последовательность чисел -ичной системы счисления и также зачастую относится к
позиционным системам счисления. Основанием смешанной системы счисления
является возрастающая последовательность чисел 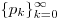 и каждое число и каждое число  представляется как
линейная комбинация: представляется как
линейная комбинация:
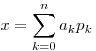 , ,
где на коэффициенты 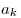 накладываются некоторые
ограничения. накладываются некоторые
ограничения.
Записью числа 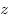 в смешанной системе счисления называется
перечисление его цифр в порядке уменьшения индекса в смешанной системе счисления называется
перечисление его цифр в порядке уменьшения индекса 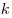 ,
начиная с первого ненулевого. ,
начиная с первого ненулевого.
Если 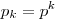 для некоторого для некоторого  , то смешанная
система счисления совпадает с , то смешанная
система счисления совпадает с  -ичной системой счисления. -ичной системой счисления.
Наиболее известным примером смешанной системы счисления являются
представление времени в виде количества суток, часов, минут и секунд.
При этом величина 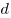 дней дней 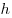 часов часов  минут
минут 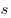 секунд соответствует значению секунд соответствует значению 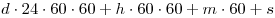 секунд.
секунд.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
