Правильные n-угольники
Правильный n-угольник — n-угольник, у которого равны все стороны и все углы.
Теорема. Все углы правильного n-угольника меньше 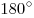 . (Если продлить любую из сторон, правильный n-угольник будет лежать по одну сторону от проведенной прямой). . (Если продлить любую из сторон, правильный n-угольник будет лежать по одну сторону от проведенной прямой).
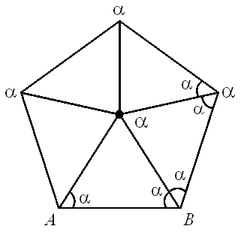
Центр правильного n-угольника — это точка, равноудаленная от всех его вершин и от всех его сторон.
Теорема. У любого правильного n-угольника есть центр.
Теорема. Вокруг правильного n-угольника можно описать только одну окружность.
Теорема (об углах правильного n-угольника):
Угол между биссектрисами двух соседних углов равен: 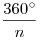 . .
Угол правильного n-угольника: 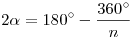 . .
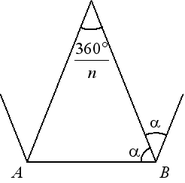
Сумма углов правильного n-угольника равна: 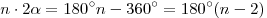 . .
Число диагоналей в правильном n-угольнике: 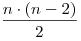 . .
Элементы правильных n-угольников:
Радиус вписанной окружности: 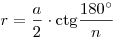 . .
Сторона правильного n-угольника: 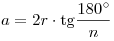 . .
Радиус описанной окружности: 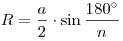 . .
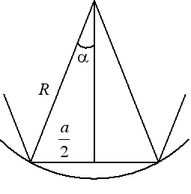
Площадь правильного n-угольника: 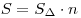 , , 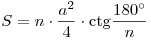 . .
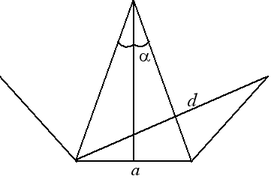
Пусть две соседние стороны правильного n-угольника и его диагональ образуют треугольник. Тогда, если длины сторон правильного n-угольника равны  , то длина этой диагонали равна: , то длина этой диагонали равна:
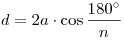 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
