Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Иными словами, скалярное произведение векторов — это число.
Если через 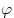 обозначить угол между векторами обозначить угол между векторами 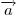 и и 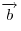 , а через , а через 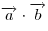 — их скалярное произведение, то — их скалярное произведение, то 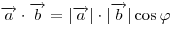 . .
Необходимым и достаточным условием перпендикулярности двух ненулевых
векторов является равенство нулю их скалярного произведения: 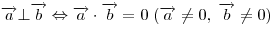 . .
Свойства скалярного произведения:
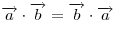 (переместительный
закон). (переместительный
закон).
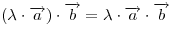 (сочетательный закон). (сочетательный закон).
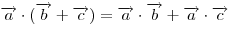 (распределительный закон). (распределительный закон).
Скалярное произведение выражается через координаты сомножителей по
формуле: 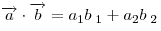 . .
Отсюда, в частности, следует:
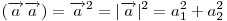 . .
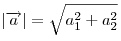 . .
Необходимым и достаточным условием перпендикулярности ненулевых векторов 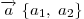 и и 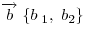 является равенство: является равенство: 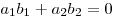 . .
Угол между векторами 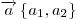 и и 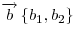 определяется по формуле: определяется по формуле:
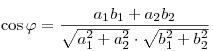 . .
Поскольку косинус острого угла положителен, а косинус тупого угла — отрицателен, то, если скалярное произведение положительно,
векторы образуют острый угол, а если отрицательно — тупой.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
