Параллелограмм, его признаки и свойства
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
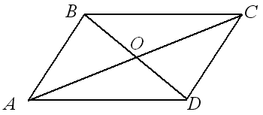
Теоремы (свойства параллелограмма):
Признаки параллелограмма:
Если противоположные стороны четырехугольника попарно параллельны, то
этот четырехугольник — параллелограмм.
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике диагонали, пересекаясь, точкой пересечения
делятся пополам, то этот четырехугольник — параллелограмм.
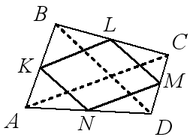
Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника 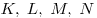 являются
вершинами параллелограмма Вариньона. являются
вершинами параллелограмма Вариньона.
Стороны этого параллелограмма параллельны соответствующим диагоналям четырехугольника  . Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь
параллелограмма Вариньона равна половине площади исходного четырехугольника. . Периметр параллелограмма Вариньона равен сумме длин диагоналей исходного четырехугольника, а площадь
параллелограмма Вариньона равна половине площади исходного четырехугольника.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
