Окружность, вписанная в многоугольник

Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.

Теоремы:

• Центром вписанной в четырехугольник окружности является точка пересечения биссектрис (если она биссектрисы всех его углов пересекаются в одной точке).

• В любом описанном четырехугольнике суммы противоположных сторон равны.

  

• Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

• Из параллелограммов окружность можно вписать в ромб, квадрат.

• Если в трапецию вписана окружность, то сумма оснований равна сумме боковых сторон, а средняя линия — полусумме боковых сторон: , .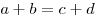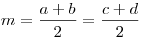

  

  
  
  Оставить комментарий
  Сообщить об ошибке