Вневписанная окружность
Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других его сторон.
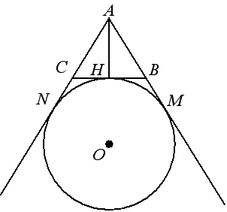
Теорема. Расстояние от вершины треугольника до точки касания вневписанной окружности с продолжением его боковой стороны равно полупериметру  : : 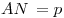 . .
Примечание: точка касания вневписанной окружности со стороной
треугольника делит его периметр пополам: 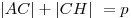 . .
Следствие: 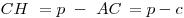 , , 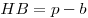 . .
Теорема. Радиус вневписанной окружности, проведенный к стороне a, вычисляется по формуле: 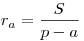 . .
Теорема. Площадь треугольника, можно вычислить по формуле: 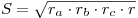 , где , где 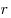 — радиус вписанной окружности; — радиус вписанной окружности; 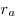 — радиус вневписанной окружности, проведенный к стороне — радиус вневписанной окружности, проведенный к стороне  ; ; 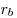 — радиус вневписанной окружности, проведенный к стороне — радиус вневписанной окружности, проведенный к стороне  ; ; 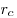 — радиус вневписанной окружности, проведенный к стороне — радиус вневписанной окружности, проведенный к стороне  . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
