Отрезки, связанные с окружностью
Теорема. Отрезки касательных к окружностям, проведенным из одной точки, равны: 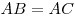 , центр окружности лежит на биссектрисе угла , центр окружности лежит на биссектрисе угла 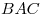 . .

Теорема. Произведение секущей на ее внешнюю часть есть для данной окружности величина постоянная и равная разности квадратов расстояния от точки пересечения секущих до центра окружности и радиуса окружности:  . .

Теорема. Произведение отрезков, на которые делится хорда данной
точкой, есть для данной окружности величина постоянная и равна разности квадратов радиуса окружности и расстояния от
точки  до центра окружности: до центра окружности:  . .

Теорема. Квадрат касательной равен произведению секущей на ее внешнюю часть:  . .

Теорема. Отношение хорды к синусу вписанного угла, который на нее опирается, равно двум радиусам (теорема синусов):  . .

Теорема Птолемея: Во всяком четырехугольнике, вписанном в
окружность, сумма произведений длин противоположных сторон равна
произведению длин его диагоналей: 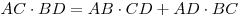 . .

 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

