Углы, связанные с окружностью
Теорема (угол между пересекающимися хордами). Угол между двумя пересекающимися хордами равен полусумме высекаемых ими дуг: 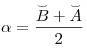 . .

Теорема (угол между секущими). Угол между двумя секущими, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг: 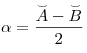 . .

Теорема (угол между касательной и хордой, проведенной через точку
касания). Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой: 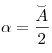 . .

Теорема (угол между касательной и секущей). Угол между касательной и секущей равен полуразности высекаемых ими дуг:
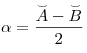 . .

Теорема (угол между касательными). Угол между двумя касательными, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг: 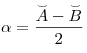 . .

 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

