Элементы окружности
Окружность — множество всех точек плоскости, удаленных на заданное расстояние (равное радиусу) от заданной точки этой же плоскости (центра окружности).
Радиусы — отрезки, соединяющие точки окружности с центром. Все радиусы данной окружности равны.

Хорда — отрезок, соединяющий любые две точки окружности.
Диаметр — хорда, проходящая через центр окружности. Диаметр, делящий хорду пополам, перпендикулярен этой хорде.
Центральный угол — угол, образованный двумя радиусами. Центральный угол измеряется дугой, на которую опирается.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны являются ее хордами.
Касательная — прямая, проходящая через точку окружности, перпендикулярно ее радиусу. Касательная имеет с окружностью только одну общую точку.
Длина окружности: 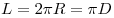 , , 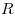 — радиус окружности, — радиус окружности, 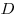 — диаметр. — диаметр.
Длина дуги окружности: 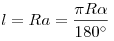 , ,  — радианная мера дуги, — радианная мера дуги, 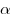 — градусная мера. — градусная мера.
Круг — часть плоскости, ограниченная окружностью.
Площадь круга: 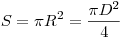 . .
Сектор — часть круга, ограниченная двумя радиусами и дугой окружности.

Площадь сектора: 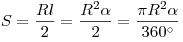 . .
Сегмент – часть круга, ограниченная хордой и дугой.

Площадь сегмента: 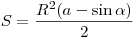 (или (или 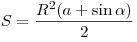 , если центр круга лежит внутри сегмента). , если центр круга лежит внутри сегмента).
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
