Теоремы об отрезках в треугольнике
Теорема Чевы. Пусть на сторонах треугольника  выбраны точки, выбраны точки,  , ,  , , 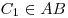 . Тогда отрезки . Тогда отрезки  пресекаются в одной точке тогда и только тогда, когда выполняется равенство: пресекаются в одной точке тогда и только тогда, когда выполняется равенство:  . .

Обобщенная теорема Чевы. Пусть прямые 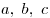 проходят через вершины проходят через вершины 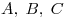 треугольника треугольника  и пересекают прямые и пересекают прямые 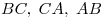 в точках в точках  соответственно. Тогда прямые соответственно. Тогда прямые 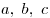 пересекаются в одной точке или параллельны тогда и только тогда, когда имеет место
равенство: пересекаются в одной точке или параллельны тогда и только тогда, когда имеет место
равенство:  . .
Теорема Менелая. Пусть дан треугольник  и точки и точки  принадлежат соответственно прямым принадлежат соответственно прямым 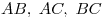 . Точки . Точки  лежат на одной прямой тогда и только тогда, когда выполняется равенство: лежат на одной прямой тогда и только тогда, когда выполняется равенство:  . .

 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
