Теоремы о площади треугольника
Площадь треугольника равна: 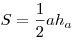 . .
Площадь треугольника равна: 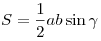 . .
Формула Герона: 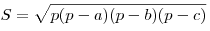 . .
Площадь треугольника равна: 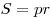 . .
Площадь треугольника равна: 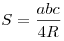 . .
Площадь треугольника равна: 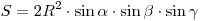 . .
Площадь треугольника равна: 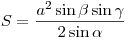 . .
Площадь треугольника равна: 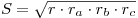 , где , где 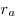 , , 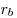 , , 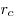 — радиусы вневписанных окружностей. — радиусы вневписанных окружностей.
Если в треугольнике одну из сторон изменить в 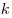 раз, а другую в раз, а другую в  раз, оставив без изменения угол между ними, то площадь получившегося треугольника измениться в раз, оставив без изменения угол между ними, то площадь получившегося треугольника измениться в 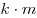 раз. раз.
Отношение площадей двух треугольников, у которых одна вершина  общая, а другие вершины расположены на двух прямых, проходящих через общая, а другие вершины расположены на двух прямых, проходящих через  , равно отношению произведений двух сторон каждого треугольника, содержащих вершину , равно отношению произведений двух сторон каждого треугольника, содержащих вершину  . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
