Прямоугольный треугольник и его свойства
Теорема Пифагора: 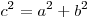 . .
Решение прямоугольного треугольника:
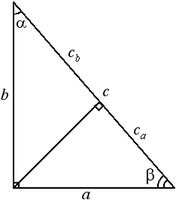
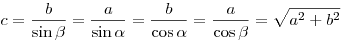 ; ;
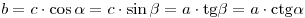 ; ;
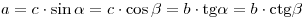 . .
Теоремы:
Высота, проведенная из вершины прямого угла, делит гипотенузу на
отрезки: 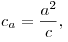 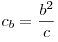 . Эти отрезки являются проекциями катетов на
гипотенузу.
Высота, проведенная из вершины прямого угла, равна среднему
геометрическому проекций катетов на гипотенузу: . Эти отрезки являются проекциями катетов на
гипотенузу.
Высота, проведенная из вершины прямого угла, равна среднему
геометрическому проекций катетов на гипотенузу: 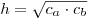 . .
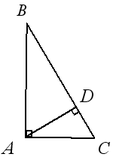
Высота в прямоугольном треугольнике, проведенная из вершины прямого
угла, делит его на два подобных и подобных исходному треугольнику. Для
любых сходственных элементов (медиана, биссектриса, радиусы вписанной и
описанной окружностей и т. п.) исходного и полученных треугольников 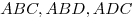 справедливо соотношение справедливо соотношение 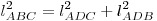 .
Длина высоты, проведенной из вершины прямого угла, равна отношению
произведения длин катетов и гипотенузы: .
Длина высоты, проведенной из вершины прямого угла, равна отношению
произведения длин катетов и гипотенузы: 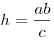 .
Медиана, проведенная из вершины прямого угла, равна половине
гипотенузы. Ее основание является центром описанной около прямоугольного треугольника окружности. Радиус описанной окружности равен этой медиане и равен половине гипотенузы: .
Медиана, проведенная из вершины прямого угла, равна половине
гипотенузы. Ее основание является центром описанной около прямоугольного треугольника окружности. Радиус описанной окружности равен этой медиане и равен половине гипотенузы: 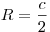 . .
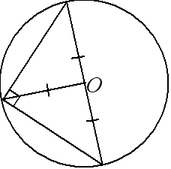
Радиус вписанной окружности равен половине суммы катетов, уменьшенной
на гипотенузы: 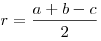 .
Площадь прямоугольного треугольника равна половине произведения
катетов: .
Площадь прямоугольного треугольника равна половине произведения
катетов: 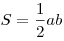 или вычисляется по любой из
следующих формул: или вычисляется по любой из
следующих формул: 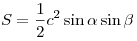 , , 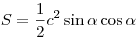 , , 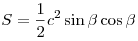 , , 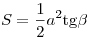 , , 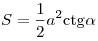 , , 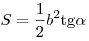 , , 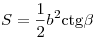 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
