Биссектриса треугольника
Биссектрисой угла называется прямая, делящая угол на две равные
части.
Биссектрисой угла треугольника называется наибольший отрезок
биссектрисы угла, лежащий внутри треугольника.
Теоремы:
Биссектриса угла треугольника — множество точек, равноудаленных от сторон угла.
Биссектриса делит сторону, к которой она проведена на отрезки, пропорциональные боковым сторонам: 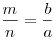 . .
Примечание. В обозначениях на рисунке имеем: 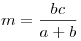 , , 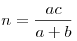 . .

Точкой пересечения биссектрисы делятся в отношении суммы сторон
треугольника, образующих угол, в котором проведена биссектриса, к
третьей стороне: 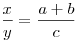 . .
Длина биссектрисы, делящей угол 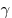 пополам, равна
удвоенному произведению сторон, деленному на их сумму и умноженному на
косинус половины угла между ними: пополам, равна
удвоенному произведению сторон, деленному на их сумму и умноженному на
косинус половины угла между ними: 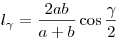 . .
Длина биссектрисы равна: 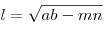 . .

Длина биссектрисы внешнего угла треугольника равна: 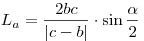 , при , при 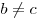 . .
Биссектрисы треугольника пересекаются в одной точке, являющейся
центром вписанной в треугольник окружности. Радиус вписанной окружности
может быть найден по формулам: 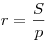 , , 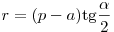 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
