Медиана треугольника
Медиана — отрезок, соединяющий вершину треугольника с серединой ее противоположной стороны.
Теоремы:
Медиана, проведенная из вершины треугольника, делит его на два равновеликих: 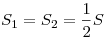 . .

Медианы пересекаются в одной точке, называемой центроидом треугольника, и точкой пересечения делятся в отношении 2:1 считая от вершины.

Отрезки медиан, соединяющие вершины с центроидом, делят треугольник на
три равновеликих: 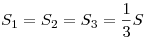 . .

Пересекаясь, медианы делят треугольник на шесть равновеликих: 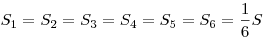 . .

Длина медианы, проведенной к стороне 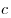 равна: равна: 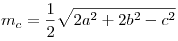 . .

 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
