Признаки равенства и подобия треугольников
Признаки равенства треугольников
Равными называют треугольники, у которых соответствующие стороны равны.
Теорема (первый признак равенства треугольников).
Если две стороны и угол, заключенный между ними, одного треугольника
соответственно равны двум сторонам и углу, заключенному между ними,
другого треугольника, то такие треугольники равны.
Теорема (второй признак равенства треугольников).
Если сторона и два прилежащих к ней угла одного треугольника
соответственно равны стороне и двум прилежащим к ней углам другого
треугольника, то такие треугольники равны.
Теорема (третий признак равенства треугольников).
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Признаки подобия треугольников
Подобными называются треугольники, у которых углы равны, а
сходственные стороны пропорциональны: 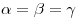 ,
, 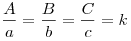 , где
, где
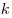 — коэффициент подобия.
— коэффициент подобия.
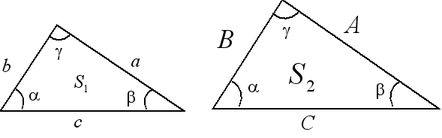
I признак подобия треугольников. Если два угла одного
треугольника соответственно равны двум углам другого, то эти
треугольники подобны.
II признак подобия треугольников. Если три стороны одного
треугольника пропорциональны трем сторонам другого треугольника, то
такие треугольники подобны.
III признак подобия треугольников. Если две стороны одного
треугольника пропорциональны двум сторонам другого треугольника, а
углы, заключенные между этими сторонами, равны, то такие треугольники
подобны.
Следствие: Площади подобных треугольников относятся как квадрат
коэффициента подобия: 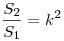 .
.
 Оставить комментарий
Оставить комментарий
 Сообщить об ошибке
Сообщить об ошибке

