Элементы треугольника
Сторона треугольника — отрезок, соединяющий две его вершины.
Неравенство треугольника — в любом треугольнике сумма длин двух сторон больше длины третьей стороны: 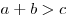 , , 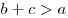 , , 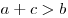 . .
Пусть 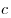 — наибольшая из трех сторон треугольника, тога если — наибольшая из трех сторон треугольника, тога если 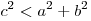 , то треугольник остроугольный; если , то треугольник остроугольный; если 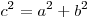 , то треугольник прямоугольный; если , то треугольник прямоугольный; если 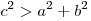 , то треугольник тупоугольный. , то треугольник тупоугольный.
Угол — часть плоскости, ограниченная двумя лучами, выходящими из вершины.
Теорема. Сумма углов треугольника равна 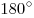 : :
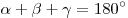 . .
Следствие: В треугольнике не может быть более одного тупого или
прямого угла.
Внешний угол — угол, смежный с каким-нибудь углом треугольника.
Теорема. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Биссектриса угла — прямая, делящая угол на две равные части.
Биссектриса угла треугольника
— наибольший отрезок биссектрисы угла, лежащий внутри треугольника.
Теорема. Если точка лежит на биссектрисе треугольника, то она
равноудалена от сторон угла.
Верно и обратное утверждение: если точка равноудалена от сторон угла, то она лежит на биссектрисе угла этого треугольника.
Биссектрисы треугольника пересекаются в одной точке, называемой инцентром, и являющейся центром вписанной в этот треугольник
окружности. Радиус вписанной в треугольник окружности может
быть найден по формулам: 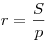 , , 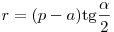 . .

Теорема синусов. Отношение длины стороны треугольника к синусу
противолежащего угла для данного треугольника есть величина постоянная
и равная диаметру описанной около треугольника окружности:
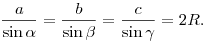
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: 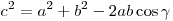 . .
Теорема тангенсов. Разность двух сторон треугольника относится
к их сумме, как тангенс полуразности противолежащих углов к тангенсу их
полусуммы: 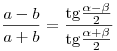 . .
Медиана — это отрезок, соединяющий какую-либо вершину треугольника с серединой противоположной стороны.
Теорема. Медианы треугольника пересекаются в одной точке,
называемой центроидом треугольника, и являющейся центром тяжести
этого треугольника.
Высота — это перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение.
Высоты треугольника пересекаются в одной точке, называемой ортоцентром. Длины высот находятся по следующим формулам:
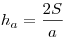 , , 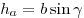 . .
Биссектриса угла треугольника лежит между медианой и высотой, проведенной из той же вершины, что и сама биссектриса.

Средняя линия треугольника — это отрезок, соединяющий
середины двух его сторон.

Теорема. Средняя линия треугольника, соединяющая середины двух
его сторон, параллельна третьей стороне и равна ее половине: 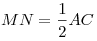 , , 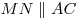 . .
Серединный перпендикуляр к отрезку — прямая, перпендикулярная к этому отрезку и проходящая через его середину.
Теорема. Если точка лежит на серединном перпендикуляре к отрезку, то она равноудалена от его концов.
Верно и обратное утверждение: если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к нему.
Все три серединных перпендикуляра пересекаются в одной точке, являющейся центром окружности, описанной вокруг треугольника.

Если треугольник остроугольный, центр описанной окружности лежит строго внутри треугольника. Если треугольник прямоугольный, центр описанной окружности лежит на середине гипотенузы. Если треугольник тупоугольный, центр описанной окружности лежит вне треугольника.
Радиус описанной окружности может быть найден по формулам: 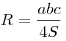 , , 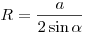 . .
Три замечательные точки треугольника: центр описанной
окружности, точка пересечения медиан и точка пересечения высот лежат на
одной прямой. Эта прямая называется прямой Эйлера.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
