В 1655 году Валлис издаёт большой трактат «Арифметика бесконечного» («Arithmetica infinilorum, sive nova methodus inquirendi curvilineorum quadratura»), где появляется придуманный им символ бесконечности: 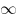. В книге он формулирует строгое определение предела переменной величины, продолжает многие идеи Декарта, впервые ввёл отрицательные абсциссы, вычисляет суммы бесконечных рядов — по существу интегральные суммы, хотя понятия интеграла тогда ещё не было. В «Трактате о конических сечениях», приложении к «Арифметике бесконечного», Валлис развил метод неделимых Кавальери, перенеся его с геометрической базы на алгебраическую. Здесь он также, в нашем понимании, вычисляет ряд определённых интегралов для степенной функции и близких к ней. Начиная с Валлиса, конические сечения рассматриваются как плоские кривые; при этом Валлис использует не только декартовы, но и косоугольные координаты. В математике Валлис всегда уделял особое внимание практически-вычислительным аспектам, зачастую пренебрегая строгими доказательствами. В 1685 году он опубликовал «Трактат по алгебре» с обстоятельной теорией логарифмов, разложения бинома и приближённых вычислений. Впервые появляются термины: мантисса, интерпретация, непрерывная дробь, интерполяция. Валлис вывел рекуррентные соотношения для подходящих дробей непрерывной дроби. Полную теорию этих дробей дал Эйлер в XVIII веке. Труды Валлиса произвели большое впечатление на молодого Ньютона. Не удивительно, что именно в письмах к Валлису Ньютон впервые открыто формулирует принципы своей версии дифференциального исчисления (1692 год). Валлис опубликовал эти письма в переиздании своего "Трактате по алгебре" (1693). Валлис первый дал современное определение логарифмирования — как операции, обратной возведению в степень. Непер, изобретатель логарифмов, определил их кинематически, затушевав их истинную природу.Одновременно с Гюйгенсом и Реном он решил вопрос об упругом соударении шаров, основываясь на законе сохранения количества движения.

Оставить комментарий
Сообщить об ошибке