|
Дед Гаусса был бедным крестьянином, отец — садовником,
каменщиком, смотрителем каналов в герцогстве Брауншвейг. Уже в
двухлетнем возрасте мальчик показал себя вундеркиндом. В три года он
умел читать и писать, даже исправлял счётные ошибки отца. Согласно
легенде, школьный учитель математики, чтобы занять детей на долгое
время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс
заметил, что попарные суммы с противоположных концов одинаковы:
1+100=101, 2+99=101 и т. д., и мгновенно получил результат
50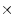 101=5050.До самой старости он привык большую часть
вычислений производить в уме. 101=5050.До самой старости он привык большую часть
вычислений производить в уме.
С учителем ему повезло: М. Бартельс (впоследствии учитель
Лобачевского) оценил исключительный талант юного Гаусса и сумел
выхлопотать ему стипендию от герцога Брауншвейгского. Это помогло
Гауссу закончить колледж Collegium Carolinum в Брауншвейге
(1792—1795).
Свободно владея множеством языков, Гаусс некоторое время колебался в
выборе между филологией и математикой, но предпочёл последнюю. Он очень
любил латинский язык и значительную часть своих трудов написал на
латыни; любил английскую, французскую и русскую литературу. В возрасте
62 года Гаусс начал изучать русский язык, чтобы ознакомиться с трудами
Лобачевского, и вполне преуспел в этом деле.
В колледже Гаусс изучил труды Ньютона, Эйлера, Лагранжа. Уже там он
сделал несколько открытий в высшей арифметике, в том числе доказал
закон взаимности квадратичных вычетов. Лежандр, правда, открыл этот
важнейший закон раньше, но строго доказать не сумел; Эйлеру это также
не удалось. Кроме этого, Гаусс создал «метод наименьших
квадратов» (тоже независимо открытый Лежандром) и начал
исследования в области «нормального распределения ошибок».
1796: Гаусс доказал возможность построения с помощью циркуля и линейки
правильного семнадцатиугольника. Более того, он разрешил проблему
построения правильных многоугольников до конца и нашёл критерий
возможности построения правильного n-угольника с помощью циркуля и
линейки: если n — простое число, то оно должно быть вида (числом
Ферма). Этим открытием Гаусс очень дорожил и завещал изобразить на его
могиле правильный 17-угольник, вписанный в круг.
1798: закончен шедевр «Арифметические исследования» (лат.
Disquisitiones Arithmeticae), напечатана только в 1801 году.
В этом труде подробно излагается теория сравнений в современных
(введенных им) обозначениях, решаются сравнения произвольного порядка,
глубоко исследуются квадратичные формы, комплексные корни из единицы
используются для построения правильных n-угольников, изложены свойства
квадратичных вычетов, приведено его доказательство квадратичного закона
взаимности и т. д. Гаусс любил говорить, что математика — царица
наук, а теория чисел — царица математики.
Герцог продолжал опекать молодого гения. Он оплатил печать его
докторской диссертации (1799) и пожаловал неплохую стипендию. В своей
докторской Гаусс впервые доказал основную теорему алгебры. До Гаусса
было много попыток это доказать, наиболее близко к цели подошёл
Д'Аламбер. Гаусс неоднократно возвращался к этой теореме и дал 4
различных доказательства её.
С 1799 года Гаусс — приват-доцент Брауншвейгского университета.
1801: избирается членом-корреспондентом Петербургской Академии наук.
Слава Гаусса становится общеевропейской. Многие научные общества
Европы избирают Гаусса своим членом, герцог увеличивает пособие, а
интерес Гаусса к астрономии ещё более возрастает.
1805: Гаусс женился. Впоследствии жена Иоганна родила ему троих детей.
1806: от раны, полученной на войне с Наполеоном, умирает его
великодушный покровитель-герцог. Несколько стран наперебой приглашают
Гаусса на службу (в том числе в Петербург). По рекомендации Александра
фон Гумбольдта Гаусса назначают профессором в Гёттингене и директором
Гёттингенской обсерватории. Эту должность он занимал до самой смерти.
1809: новый шедевр, «Теория движения небесных тел».
Изложена каноническая теория учёта возмущений орбит.
Как раз в четвёртую годовщину свадьбы умирает Иоганна. В Германии
разруха и анархия. Самые тяжёлые годы для Гаусса. 1810 г. - новая
женитьба, на подруге Иоганны. Число детей Гаусса вскоре увеличивается
до шести.
1810: новые почести. Гаусс получает премию Парижской академии наук и
золотую медаль Лондонского королевского общества.
1811: появляется новая комета. Гаусс быстро и очень точно рассчитывает
её орбиту. Начинает работу над комплексным анализом, открывает (но не
публикует) теорему, позже переоткрытую Коши и Вейерштрассом: интеграл
от аналитической функции по замкнутому контуру равен нулю.
1812: исследование гипергеометрического ряда, обобщающего разложение
практически всех известных тогда функций.
Знаменитую комету «пожара Москвы» (1812) всюду наблюдают,
пользуясь вычислениями Гаусса.
1815: публикует первое строгое доказательство основной теоремы
алгебры.
1821: в связи с работами по геодезии Гаусс начинает исторический цикл
работ по теории поверхностей. В науку входит «гауссова
кривизна». Положено начало дифференциальной геометрии. Именно
результаты Гаусса вдохновили Римана на его классическую диссертацию о
«римановой геометрии».
Итогом изысканий Гаусса была работа «Исследования относительно
кривых поверхностей» (1822). В ней свободно используются общие
криволинейные координаты на поверхности. Гаусс далеко развил метод
конформного отображения, которое в картографии сохраняет углы (но
искажает расстояния); оно применяется также в аэро/гидродинамике и
электростатике.
1824: избирается иностранным членом Петербургской Академии наук.
1825: открывает гауссовы комплексные целые числа, строит для них
теорию делимости и сравнений. Успешно применяет их для решения
сравнений высоких степеней.
1831: умирает вторая жена, у Гаусса начинается тяжелейшая бессонница.
В Геттинген приезжает приглашённый по инициативе Гаусса 27-летний
талантливый физик Вильгельм Вебер, с которым Гаусс познакомился в 1828
году, в гостях у Гумбольдта. Оба энтузиаста науки сдружились, несмотря
на разницу в возрасте, и начинают цикл исследований электромагнетизма.
1833: Гаусс изобретает электрический телеграф и (вместе с Вебером)
строит его действующую модель.
1839: 62-летний Гаусс овладевает русским языком и в письмах в
Петербургскую Академию просит прислать ему русские журналы и книги, в
частности «Капитанскую дочку» Пушкина. Предполагают, что
это связано с работами Лобачевского. В 1842 году по рекомендации Гаусса
Лобачевский избирается иностранным членом-корреспондентом
Гёттингенского королевского общества.
Умер Гаусс 23 февраля 1855 года в Гёттингене.
Современники вспоминают Гаусса как жизнерадостного, дружелюбного
человека, с отличным чувством юмора.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
