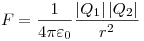
|
Закон Кулона, где 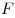 — сила
взаимодействия
двух точечных зарядов — сила
взаимодействия
двух точечных зарядов 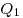 и и 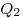 в
вакууме, в
вакууме,
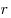 — расстояние между зарядами, — расстояние между зарядами,
 — электрическая постоянная. — электрическая постоянная.
|
|
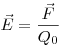
|
Напряженность электростатического поля, где 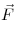 — сила, действующая на точечный положительный заряд
— сила, действующая на точечный положительный заряд
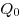 , помещенный в данную точку поля. , помещенный в данную точку поля.
|
|
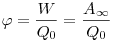
|
Потенциал электростатического поля, где 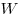 —
потенциальная энергия заряда
—
потенциальная энергия заряда 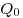 , ,
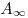 — работа по перемещению заряда из данной точки поля
за его
пределы (на бесконечность).
— работа по перемещению заряда из данной точки поля
за его
пределы (на бесконечность).
|
|
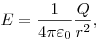
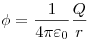
|
Напряженность 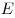 и потенциал и потенциал 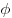 электростатического поля точечного заряда на расстоянии
электростатического поля точечного заряда на расстоянии
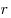 от
заряда. от
заряда.
|
|
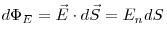
|
Поток вектора напряженности 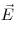 через
площадку через
площадку
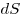 , где , где 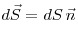 —
вектор
площадки, модуль которого равен —
вектор
площадки, модуль которого равен 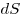 , а
направление совпадает
с нормалью , а
направление совпадает
с нормалью 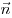 к площадке, к площадке, 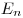 —
проекция вектора
—
проекция вектора 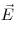 на нормаль на нормаль 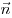 к
площадке к
площадке 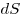 . .
|
|
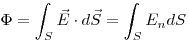
|
Поток вектора напряженности 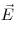 через
произвольную поверхность через
произвольную поверхность  . .
|
|
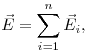
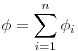
|
Принцип суперпозиции электростатических полей, где 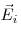 и и 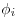 — напряженность и потенциал
поля, создаваемого зарядом — напряженность и потенциал
поля, создаваемого зарядом 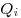 , соответственно. , соответственно.
|
|
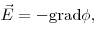
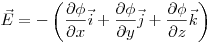
|
Связь между напряженностью 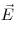 и потенциалом
электростатического поля и потенциалом
электростатического поля 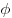 , где , где 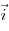 , ,
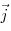 , , 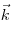 — единичные
векторы
координаты осей. — единичные
векторы
координаты осей.
|
|
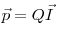
|
Электрический момент диполя (дипольный момент), где
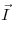 — плечо диполя. — плечо диполя.
|
|
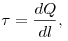
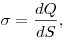
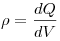
|
Линейная, поверхностная и объемная плотности зарядов.
|
|
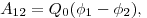
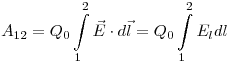
|
Работа, совершаемая силами электростатического поля при
перемещении заряда 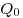 из точки 1 в точку 2,
где из точки 1 в точку 2,
где 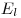 — проекция вектора — проекция вектора 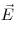 на
направление
элементарного перемещения на
направление
элементарного перемещения 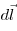 . .
|
|
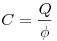
|
Электроемкость уединенного проводника, где 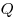 — заряд, сообщенный проводнику,
— заряд, сообщенный проводнику, 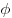 —
потенциал проводника.
—
потенциал проводника.
|
|
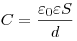
|
Емкость плоского конденсатора, где  —
площадь каждой пластины конденсатора, —
площадь каждой пластины конденсатора, 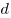 —
расстояние
между пластинами. —
расстояние
между пластинами.
|
|
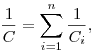
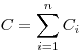
|
Емкость системы конденсаторов при последовательном и
параллельном соединениях соответственно, где 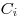 —
емкость —
емкость 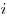 -того конденсатора, -того конденсатора,  — число
конденсаторов.
— число
конденсаторов.
|
|
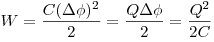
|
Энергия уединенного заряженного проводника.
|
|
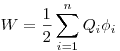
|
Энергия взаимодействия системы точечных зарядов, где
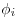 — потенциал, создаваемый в той точке, где
находится
заряд — потенциал, создаваемый в той точке, где
находится
заряд 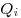 , всеми зарядами кроме , всеми зарядами кроме
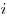 -того. -того.
|
|
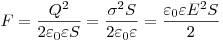
|
Сила притяжения между двумя разноименного заряженными
обкладками конденсатора.
|
|
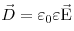
|
Связь между векторами электрического смещения 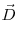 и напряженностью электростатического поля и напряженностью электростатического поля
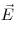 ,
где ,
где 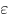 — диэлектрическая
проницаемость
среды, — диэлектрическая
проницаемость
среды,  — электрическая
постоянная. — электрическая
постоянная.
|

