 (при (при  ) )
|
Закон Бойля-Мариотта, где  — давление, — давление,
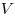 — объем, — объем, 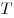 — термодинамическая
температура (изотермический процесс). — термодинамическая
температура (изотермический процесс).
|
|
 (при (при  ) )
|
Закон Гей-Люссака (изобарный процесс).
|
|
 (при (при  ) )
|
Закон Шарля (изохорный процесс).
|
|

|
Закон Дальтона для давления смеси  идеальных
газов, где идеальных
газов, где  — парциальное давление — парциальное давление
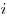 -того компонента смеси. -того компонента смеси.
|
|

|
Уравнение состояния идеального газа (уравнение
Клайперона-Менделеева), где 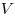 — объем газа, — объем газа,
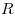 — молярная газовая постоянная, — молярная газовая постоянная, 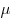 — молярная масса газа,
— молярная масса газа,  — масса газа, — масса газа,
 — количество вещества. — количество вещества.
|
|

|
Зависимость давления газа от концентрации  молекул
и температуры молекул
и температуры 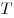 , где , где 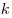 — постоянная
Больцмана ( — постоянная
Больцмана (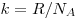 , , 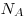 — постоянная
Авогадро). — постоянная
Авогадро).
|
|

|
Средняя кинетическая энергия поступательного движения молекул
идеального газа.
|
|

|
Барометрическая формула, где  и и  — давление газа на высоте
— давление газа на высоте  и и 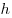 . .
|
|


|
Распределение Больцмана по во внешнем потенциальном поле, где
 и и  — концентрация молекул на высоте — концентрация молекул на высоте
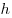 и и  , ,  —
потенциальная энергия молекул в поле тяготения. —
потенциальная энергия молекул в поле тяготения.
|
|

|
Закон Ньютона для внутреннего трения (вязкости), где
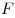 — сила внутреннего трения между движущимися слоями
площадью — сила внутреннего трения между движущимися слоями
площадью  , ,  — градиент скорости, — градиент скорости,
 — динамическая вязкость. — динамическая вязкость.
|

