Физика → Теория → Справочник → Основные формулы и законы курса физики → Физические основы механики → Динамика частицы и поступательного движения твердого тела

Динамика частицы и поступательного движения твердого тела

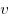$\vec p = m\vec v$ Импульс (количество движения) материальной точки (частицы), — масса и — скорость частицы.

$\vec F = m\vec a = m\frac{{d\vec v}}{{dt}} = \frac{{d\vec p}}{{dt}}$ Второй закон Ньютона (основное уравнение динамики частицы), где $\vec F = \sum\limits_i {\vec F_i }$ — сумма всех сил, действующих на частицу.

$F_{} = \mu N$ Сила трения скольжения, где 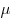$\mu$ — коэффициент трения скольжения, 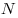— сила нормального давления.

$F_{} = \frac{{k_r N}}{r}$ Сила трения качения, где k_r — коэффициент трения качения, 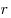— радиус катящегося тела.

$\vec p = \sum\limits_{i = 1}^n {m_i \vec v_i = const}$ Закон сохранения импульса для замкнутой системы, где — число частиц (или тел), входящих в систему.

$x_c = \frac{{\sum m _i x_i }}{{\sum {m_i } }},$

$y_c = \frac{{\sum {m_i y_i } }}{{\sum {m_i } }},$

$z_c = \frac{{\sum {m_i z_i } }}{{\sum {m_i } }}$ Координаты центра масс системы частиц, где m_i — масса i-той частицы, x_i
, y_i
, z_i — ее координаты.

$m\vec a = \vec F - \vec u\frac{{dm}}{{dt}}$ Уравнение движения тела переменной массы (уравнение Мещерского), где $\vec F_$ — реактивная сила, $\vec u$ — скорость истечения газов из ракеты, — масса ракеты.

$v = u\ln \frac{{m_0 }}{m}$ Формула Циолковского для определения скорости ракеты, где m_0 — начальная масса ракеты.

Оставить комментарий
Сообщить об ошибке