|
Единый государственный экзамен по физике, 2009 год,
демонстрационная версия
Скачать pdf-файл.
Часть A
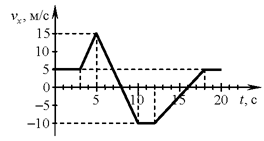 А1. На рисунке приведён график зависимости проекции скорости тела от времени. График зависимости проекции ускорения тела А1. На рисунке приведён график зависимости проекции скорости тела от времени. График зависимости проекции ускорения тела 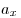 от времени в интервале времени от 12 до 16 с совпадает с графиком от времени в интервале времени от 12 до 16 с совпадает с графиком
Решение. Из графика видно, что в интервале времени от 12 до 16
с скорость менялась равномерно от –10 м/с до 0 м/с.
Ускорение было постоянным и равным
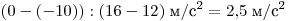 . .
График ускорения представлен на четвёртом рисунке.
Правильный ответ: 4.
А2. Полосовой магнит массой m поднесли к массивной стальной плите массой M. Сравните силу действия магнита на плиту 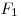 с силой действия плиты на магнит с силой действия плиты на магнит 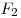 . .
Решение. По третьему закону Ньютона сила, с которой магнит действует на плиту, равна силе, с которой плита действует на магнит.
Правильный ответ: 1.
А3. При движении по горизонтальной поверхности на тело массой
40 кг действует сила трения скольжения 10 Н. Какой станет сила трения
скольжения после уменьшения массы тела в 5 раз, если коэффициент трения
не изменится?
|
1)
|
1 Н
| |
2)
|
2 Н
| |
3)
|
4 Н
| |
4)
|
8 Н
|
Решение. При уменьшении массы тела в 5 раз вес тела также уменьшится в 5 раз. Значит, и сила трения скольжения уменьшится в 5 раз и составит 2 Н.
Правильный ответ: 2.
А4. Легковой автомобиль и грузовик движутся со скоростями 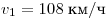 и и 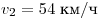 . Масса легкового автомобиля m = 1000 кг. Какова масса грузовика, если отношение импульса грузовика к импульсу легкового автомобиля равно 1,5? . Масса легкового автомобиля m = 1000 кг. Какова масса грузовика, если отношение импульса грузовика к импульсу легкового автомобиля равно 1,5?
|
1)
|
3000 кг
| |
2)
|
4500 кг
| |
3)
|
1500 кг
| |
4)
|
1000 кг
|
Решение. Импульс автомобиля равен 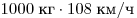 . Импульс грузовика в 1,5 раза больше. Масса
грузовика равна . Импульс грузовика в 1,5 раза больше. Масса
грузовика равна 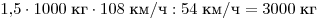 . .
Правильный ответ: 1.
А5. Санки массой m тянут в гору с постоянной скоростью.
Когда санки поднимутся на высоту h от первоначального положения,
их полная механическая энергия
|
1)
|
не изменится
| |
2)
|
увеличится на mgh
| |
3)
|
будет неизвестна, так как не задан наклон горки
| |
4)
|
будет неизвестна, так как не задан коэффициент трения
|
Решение. Поскольку санки тянут с постоянной скоростью, их
кинетическая энергия не меняется. Изменение полной механической энергии
санок равно изменению их потенциальной энергии. Полная механическая
энергия увеличится на mgh.
Правильный ответ: 2.
А6. Принято считать, что женский голос сопрано занимает
частотный интервал от 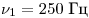 до до 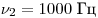 . Отношение граничных длин звуковых волн . Отношение граничных длин звуковых волн
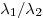 этого интервала равно этого интервала равно
|
1)
|
1
| |
2)
|
2
| |
3)
|
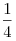
| |
4)
|
4
|
Решение. Отношение длин волн обратно пропорционально отношению
частот: 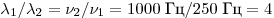 . .
Правильный ответ: 4.
А7. На фотографии показана установка для исследования
равноускоренного скольжения каретки (1) массой 0,1 кг по наклонной
плоскости, установленной под углом 30° к горизонту.
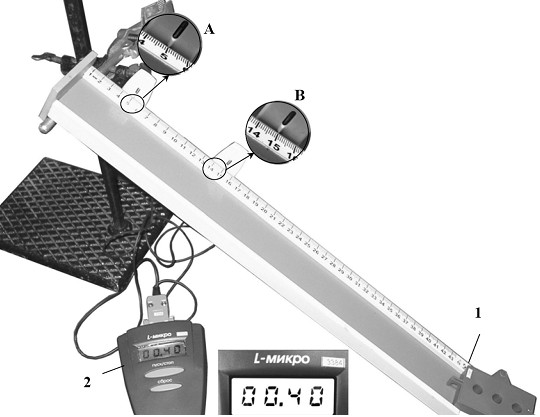
В момент начала движения верхний датчик (А) включает секундомер (2), а
при прохождении каретки мимо нижнего датчика (В) секундомер
выключается. Числа на линейке обозначают длину в сантиметрах. Какое
выражение описывает зависимость скорости каретки от времени? (Все
величины указаны в единицах СИ.)
Решение. Из рисунка видно, что за время
t = 0,4 с каретка прошло путь
s = 0,1 м. Поскольку начальная скорость каретки равна
нулю, можно определить её ускорение:
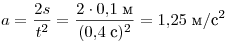 . .
Таким образом, скорость каретки зависит от времени по закону 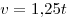 . .
Правильный ответ: 1.
А8. При понижении абсолютной температуры одноатомного
идеального газа в 1,5 раза средняя кинетическая энергия теплового
движения его молекул
|
1)
|
увеличится в 1,5 раза
| |
2)
|
уменьшится в 1,5 раза
| |
3)
|
уменьшится в 2,25 раза
| |
4)
|
не изменится
|
Решение. Средняя кинетическая энергия теплового движения
молекул идеального газа прямо пропорциональна абсолютной температуре.
При понижении абсолютной температуры в 1,5 раза средняя
кинетическая энергия также уменьшится в 1,5 раза.
Правильный ответ: 2.
А9. Горячая жидкость медленно охлаждалась в стакане. В таблице
приведены результаты измерений её температуры с течением времени.
|
Время, мин
|
0
|
2
|
4
|
6
|
8
|
10
|
12
|
14
|
|
Температура, °С
|
95
|
88
|
81
|
80
|
80
|
80
|
77
|
72
|
В стакане через 7 мин после начала измерений находилось вещество
|
1)
|
только в жидком состоянии
| |
2)
|
только в твёрдом состоянии
| |
3)
|
и в жидком, и в твёрдом состояниях
| |
4)
|
и в жидком, и в газообразном состояниях
|
Решение. Из таблицы видно, что в период времени между шестой и
десятой минутой температура в стакане оставалась постоянной. Значит, в
это время проходила кристаллизация (затвердевание) жидкости; вещество в
стакане находилось одновременно и в жидком, и в твёрдом состояниях.
Правильный ответ: 3.
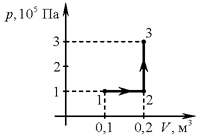 А10. Какую работу совершает газ при переходе из состояния 1 в
состояние 3 (см. рисунок)? А10. Какую работу совершает газ при переходе из состояния 1 в
состояние 3 (см. рисунок)?
|
1)
|
10 кДж
| |
2)
|
20 кДж
| |
3)
|
30 кДж
| |
4)
|
40 кДж
|
Решение. Процесс 1–2 изобарический: давление газа равно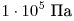 , объём увеличивается на , объём увеличивается на
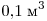 , газ при этом совершает работу , газ при этом совершает работу 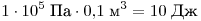 . Процесс
2–3 изохорный: газ работу не совершает. В итоге, при переходе из
состояния 1 в состояние 3 газ совершает работу 10 кДж. . Процесс
2–3 изохорный: газ работу не совершает. В итоге, при переходе из
состояния 1 в состояние 3 газ совершает работу 10 кДж.
Правильный ответ: 1.
А11. В тепловой машине температура нагревателя 600 K,
температура холодильника на 200 K меньше, чем у нагревателя.
Максимально возможный КПД машины равен
Решение. Максимально возможный КПД тепловой машины равен КПД
машины Карно:
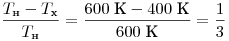 . .
Правильный ответ: 4.
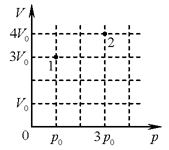 А12. В сосуде находится постоянное количество идеального газа.
Как изменится температура газа, если он перейдёт из состояния 1 в
состояние 2 (см. рисунок)? А12. В сосуде находится постоянное количество идеального газа.
Как изменится температура газа, если он перейдёт из состояния 1 в
состояние 2 (см. рисунок)?
Решение. Согласно уравнению состояния идеального газа при
постоянном количестве газа
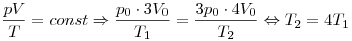 . .
Правильный ответ: 1.
А13. Расстояние между двумя точечными электрическими зарядами
уменьшили в 3 раза, а один из зарядов увеличили в 3 раза. Силы
взаимодействия между ними
|
1)
|
не изменились
| |
2)
|
уменьшились в 3 раза
| |
3)
|
увеличились в 3 раза
| |
4)
|
увеличились в 27 раз
|
Решение. При уменьшении расстояния между двумя точечными
электрическими зарядами в 3 раза сила взаимодействия между ними
возрастает в 9 раз. Увеличение одного из зарядов в 3 раза приводит
к такому же увеличению силы. В итоге сила их взаимодействия стала в 27
раз больше.
Правильный ответ: 4.
 А14. Каким будет сопротивление участка цепи (см. рисунок), если
ключ К замкнуть? (Каждый из резисторов имеет сопротивление R.) А14. Каким будет сопротивление участка цепи (см. рисунок), если
ключ К замкнуть? (Каждый из резисторов имеет сопротивление R.)
Решение. После замыкания ключа клеммы окажутся закороченными,
сопротивление этого участка цепи станет равным нулю.
Правильный ответ: 4.
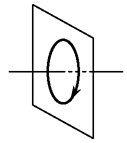 А15. На рисунке изображен проволочный виток, по которому течёт
электрический ток в направлении, указанном стрелкой. Виток расположен в
вертикальной плоскости. В центре витка вектор индукции магнитного поля
тока направлен А15. На рисунке изображен проволочный виток, по которому течёт
электрический ток в направлении, указанном стрелкой. Виток расположен в
вертикальной плоскости. В центре витка вектор индукции магнитного поля
тока направлен
|
1)
|
вертикально вверх 
| |
2)
|
вертикально вниз 
| |
3)
|
горизонтально вправо 
| |
4)
|
горизонтально влево 
|
Решение. По правилу правой руки: «Если обхватить соленоид
(виток с током) ладонью правой руки так, чтобы четыре пальца были
направлены вдоль тока в витках, то отставленный большой палец покажет
направление линий магнитного поля внутри соленоида (витка с
током)». Мысленно проделав указанные действия, получаем, что в
центре витка вектор индукции магнитного поля направлен горизонтально
вправо.
Правильный ответ: 3.
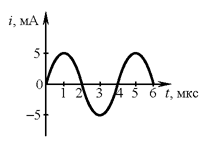 А16. На рисунке приведен график гармонических колебаний тока в
колебательном контуре. Если катушку в этом контуре заменить другой
катушкой, индуктивность которой в 4 раза меньше, то период колебаний
станет равен А16. На рисунке приведен график гармонических колебаний тока в
колебательном контуре. Если катушку в этом контуре заменить другой
катушкой, индуктивность которой в 4 раза меньше, то период колебаний
станет равен
|
1)
|
1 мкс
| |
2)
|
2 мкс
| |
3)
|
4 мкс
| |
4)
|
8 мкс
|
Решение. Из графика видно, что период колебаний тока в
колебательном контуре равен 4 мкс. При уменьшении индуктивности катушки
в 4 раза, период уменьшится в 2 раза. После замены катушки он станет
равным 2 мкс.
Правильный ответ: 2.
А17. Источник света S отражается в плоском зеркале ab.
Изображение S этого источника в зеркале показано на рисунке
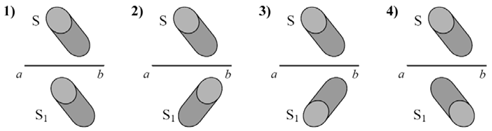
Решение. Изображение объекта, полученное с помощью плоского
зеркала, расположено симметрично объекту относительно плоскости
зеркала. Изображение  источника S в зеркале
показано на рисунке 3. источника S в зеркале
показано на рисунке 3.
Правильный ответ: 3.
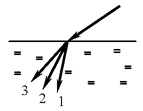 А18. В некотором спектральном диапазоне угол преломления лучей
на границе воздух — стекло падает с увеличением частоты
излучения. Ход лучей для трёх основных цветов при падении белого света
из воздуха на границу раздела показан на рисунке. Цифрам соответствуют
цвета А18. В некотором спектральном диапазоне угол преломления лучей
на границе воздух — стекло падает с увеличением частоты
излучения. Ход лучей для трёх основных цветов при падении белого света
из воздуха на границу раздела показан на рисунке. Цифрам соответствуют
цвета
|
1)
|
1 — красный
2 — зелёный
3 — синий
| |
2)
|
1 — синий
2 — красный
3 — зелёный
| |
3)
|
1 — красный
2 — синий
3 — зелёный
| |
4)
|
1 — синий
2 — зелёный
3 — красный
|
Решение. Из-за дисперсии света при переходе из воздуха в стекло
луч тем сильнее отклоняется от первоначального направления, чем меньшей
его длина волны. У синего цвета самая маленькая длина волны, у красного
— самая большая. Синий луч отклонится сильнее всего (1 —
синий), красный луч отклонится слабее всего (3 — красный),
остаётся 2 — зелёный.
Правильный ответ: 4.
А19. На входе в электрическую цепь квартиры стоит
предохранитель, размыкающий цепь при силе тока 10 А. Подаваемое в
цепь напряжение равно 110 В. Какое максимальное число
электрических чайников, мощность каждого из которых равна 400 Вт,
можно одновременно включить в квартире?
Решение. Через каждый чайник проходит электрический ток с силой 400 Вт : 110 В 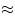 3,64 А. При включении двух чайников сила суммарная сила тока (2 3,64 А. При включении двух чайников сила суммарная сила тока (2  3,64 А = 7,28 А) будет меньше 10 А, а при включении трёх чайников — больше 10 А (3 3,64 А = 7,28 А) будет меньше 10 А, а при включении трёх чайников — больше 10 А (3  3,64 А = 10,92 А).
Одновременно можно включить не более двух чайников. 3,64 А = 10,92 А).
Одновременно можно включить не более двух чайников.
Правильный ответ: 2.
А20. На рисунке изображены схемы четырех атомов,
соответствующие модели атома Резерфорда. Чёрными точками обозначены
электроны. Атому 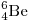 соответствует схема соответствует схема
Решение. Число электронов в нейтральном атоме совпадает с
числом протонов, которое записывается внизу перед наименованием
элемента. В атоме 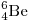 4 электрона. 4 электрона.
Правильный ответ: 1.
А21. Период полураспада ядер атомов радия
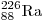 составляет 1620 лет.
Это означает, что в образце, содержащем большое число атомов радия, составляет 1620 лет.
Это означает, что в образце, содержащем большое число атомов радия,
|
1)
|
за 1620 лет атомный номер каждого атома радия уменьшится вдвое
| |
2)
|
одно ядро радия распадается каждые 1620 лет
| |
3)
|
половина изначально имевшихся ядер радия распадается за 1620 лет
| |
4)
|
все изначально имевшиеся ядра радия распадутся через 3240 лет
|
Решение. Верным является утверждение, что половина изначально
имевшихся ядер радия распадается за 1620 лет.
Правильный ответ: 3.
А22. Радиоактивный свинец 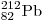 , испытав один α-распад и два β-распада,
превратился в изотоп , испытав один α-распад и два β-распада,
превратился в изотоп
|
1)
|
висмута 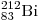
| |
2)
|
полония 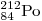
| |
3)
|
свинца 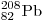
| |
4)
|
таллия 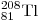
|
Решение. При α-распаде масса ядра уменьшается на 4 а. е.
м., а при β-распаде масса не изменяется. После одного
α-распад и двух β-распада масса ядра уменьшится на 4 а. е. м.
При α-распаде заряд ядра уменьшается на 2 элементарных заряда, а
при β-распаде заряд увеличивается на 1 элементарный заряд. После
одного α-распад и двух β-распада заряд ядра не изменится.
В итоге, 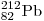 превратится
в изотоп свинца превратится
в изотоп свинца 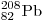 . .
Правильный ответ: 3.
А23. Фотоэффект наблюдают, освещая поверхность металла светом
фиксированной частоты. При этом задерживающая разность потенциалов
равна U. После изменения частоты света задерживающая разность
потенциалов увеличилась на ΔU = 1,2 В. На
сколько изменилась частота падающего света?
Решение. Запишем уравнение Эйнштейна для фотоэффекта для
начальной частоты света 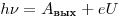 и для
изменённой частоты и для
изменённой частоты 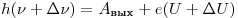 . Вычтя из второго равенства первое, получим
соотношение: . Вычтя из второго равенства первое, получим
соотношение:
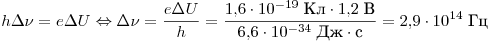 . .
Правильный ответ: 2.
А24. Проводники изготовлены из одного и того же материала.
Какую пару проводников нужно выбрать, чтобы на опыте обнаружить
зависимость сопротивления проволоки от её диаметра?
Решение. Чтобы на опыте обнаружить зависимость сопротивления
проволоки от её диаметра, нужно взять пару проводников, отличающихся
только толщиной. Длина проводников должна быть одинаковой. Нужно
взять третью пару проводников.
Правильный ответ: 3.
А25. Исследовалась зависимость напряжения на обкладках
воздушного конденсатора от заряда этого конденсатора. Результаты
измерений представлены в таблице.
|
q, мкКл
|
0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
|
U, кВ
|
0
|
0,5
|
1,5
|
3,0
|
3,5
|
3,5
|
Погрешности измерений величин q и U равнялись соответственно 0,05 мкКл и 0,25 кВ. Ёмкость конденсатора
примерно равна
|
1)
|
250 пФ
| |
2)
|
10 нФ
| |
3)
|
100 пФ
| |
4)
|
750 мкФ
|
Решение. Рассчитаем для каждого измерения величину ёмкости
конденсатора (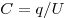 ) и усредним получившиеся значения. ) и усредним получившиеся значения.
|
q, мкКл
|
0
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
|
|
U, кВ
|
0
|
0,5
|
1,5
|
3,0
|
3,5
|
3,5
|
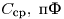
|
|
С, пФ
|
—
|
200
|
133
|
100
|
114
|
142
|
140
|
Рассчитанное значение ёмкости ближе всего к третьему варианту ответа.
Правильный ответ: 3.
Часть B
В1. Груз массой m, подвешенный на пружине, совершает
гармонические колебания с периодом T и амплитудой 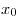 . Что произойдёт с максимальной потенциальной энергией пружины,
периодом и частотой колебаний, если при неизменной амплитуде уменьшить
массу груза? . Что произойдёт с максимальной потенциальной энергией пружины,
периодом и частотой колебаний, если при неизменной амплитуде уменьшить
массу груза?
К каждой позиции первого столбца подберите соответствующую позицию
второго и запишите в таблицу выбранные цифры под соответствующими
буквами.
|
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
|
ИХ ИЗМЕНЕНИЕ
| |
А) период колебаний
|
1) увеличится
| |
Б) частота колебаний
|
2) уменьшится
| |
В) максимальная потенциальная энергия пружины
|
3) не изменится
|
Получившуюся последовательность цифр перенесите в бланк ответов (без пробелов).
Решение. Период колебаний связан с массой груза и жёсткостью пружины k соотношением
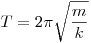 . .
При уменьшении массы период колебаний уменьшится (А — 2).
Частота обратно пропорциональная периоду, значит, частота увеличится (Б
— 1). Максимальная потенциальная энергия пружины равна
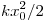 , при неизменной амплитуде колебаний она не
изменится (В — 3). , при неизменной амплитуде колебаний она не
изменится (В — 3).
Ответ: 213.
В2. Используя первый закон термодинамики, установите
соответствие между описанными в первом столбце особенностями
изопроцесса в идеальном газе и его названием.
|
ОСОБЕННОСТИ ИЗОПРОЦЕССА
|
|
НАЗВАНИЕ ИЗОПРОЦЕССА
| |
А) Всё переданное газу количество теплоты идёт на совершение
работы, а внутренняя энергия газа остаётся неизменной.
|
|
1) изотермический
2) изобарный
3) изохорный
4) адиабатный
| |
Б) Изменение внутренней энергии газа происходит только за счёт
совершения работы, так как теплообмен с окружающими телами отсутствует.
|
|
Получившуюся последовательность цифр перенесите в бланк ответов (без
пробелов и каких-либо символов).
Решение. Внутренняя энергия идеальная газа остаётся неизменной
при неизменной температуре газа, то есть, в изотермическом процессе (А
— 1). Теплообмен с окружающими телами отсутствует в
адиабатическом процессе (Б — 4).
Ответ: 14.
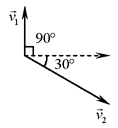 В3. Летящий снаряд разрывается на два осколка. По отношению к
направлению движения снаряда первый осколок летит под углом 90° со
скоростью 50 м/с, а второй — под углом 30° со скоростью
100 м/с. Найдите отношение массы первого осколка к массе второго
осколка. В3. Летящий снаряд разрывается на два осколка. По отношению к
направлению движения снаряда первый осколок летит под углом 90° со
скоростью 50 м/с, а второй — под углом 30° со скоростью
100 м/с. Найдите отношение массы первого осколка к массе второго
осколка.
Решение. Изобразим направления движения снаряда и двух осколков
(см. рисунок). Запишем закон сохранения проекции импульса на ось,
перпендикулярную направлению движения снаряда:
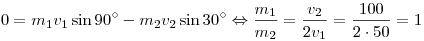 . .
Ответ: 1.
В4. В теплоизолированный сосуд с большим количеством льда при
температуре 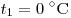 заливают
m = 1 кг воды с температурой заливают
m = 1 кг воды с температурой 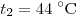 . Какая масса льда Δm расплавится
при установлении теплового равновесия в сосуде? Ответ выразите в
граммах. . Какая масса льда Δm расплавится
при установлении теплового равновесия в сосуде? Ответ выразите в
граммах.
Решение. При охлаждении вода отдаст количество теплоты 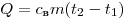 . Эта теплота растопит лёд массой . Эта теплота растопит лёд массой
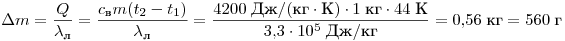 . .
Ответ: 560.
В5. Предмет высотой 6 см расположен на главной оптической оси
тонкой собирающей линзы на расстоянии 30 см от её оптического центра.
Оптическая сила линзы 5 дптр. Найдите высоту изображения предмета.
Ответ выразите в сантиметрах (см).
Решение. Обозначим высоту предмета
h = 6 см, расстояние от линзы до предмета
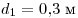 , оптическую сила линзы
D = 5 дптр. Используя формулу для тонкой линзы,
определим положение изображения предмета: , оптическую сила линзы
D = 5 дптр. Используя формулу для тонкой линзы,
определим положение изображения предмета:
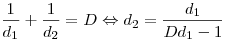 . .
Увеличение составит
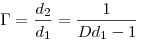 . .
Высота изображения равна
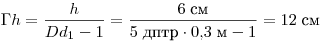 . .
Ответ: 12.
Часть C
С1. Человек в очках вошёл с улицы в теплую комнату и обнаружил, что его очки запотели. Какой должна быть температура на улице, чтобы наблюдалось это явление? В комнате температура воздуха
22 °С, а относительная влажность воздуха 50 %. Поясните, как вы получили ответ.
(При ответе на этот вопрос воспользуйтесь таблицей для давления насыщенных паров воды.)
Давление насыщенных паров воды при различных температурах
|
t, °С
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
p, кПа
|
1,07
|
1,15
|
1,23
|
1,31
|
1,40
|
1,50
|
1,60
|
1,70
|
|
t, °С
|
16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
|
p, кПа
|
1,82
|
1,94
|
2,06
|
2,20
|
2,34
|
2,49
|
2,64
|
2,81
|
Решение. Из таблицы находим, что давление насыщенных паров
в комнате составляет 2,64 кПа. Поскольку относительная влажность
воздуха равна 50 %, парциальное давление паров воды в комнате
равно 2,164 кПа 50 % = 1,32 кПа. 50 % = 1,32 кПа.
В первый момент, как человек вошёл с улицы, его очки имеют уличную
температуру. Комнатный воздух, соприкасаясь с очками, охлаждается. Из
таблицы видно, что если комнатный воздух охладится до 11 °С
или ниже, когда парциальное давление паров воды станет больше давления
насыщенных паров, пары воды конденсируются — очки запотеют.
Температура на улице должна быть не выше 11 °С.
Ответ: не выше 11 °С.
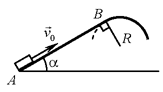 С2. Небольшая шайба после удара скользит вверх по
наклонной плоскости из точки А (см. рисунок). В точке В наклонная плоскость без излома переходит в наружную поверхность
горизонтальной трубы радиусом R. Если в точке А скорость
шайбы превосходит С2. Небольшая шайба после удара скользит вверх по
наклонной плоскости из точки А (см. рисунок). В точке В наклонная плоскость без излома переходит в наружную поверхность
горизонтальной трубы радиусом R. Если в точке А скорость
шайбы превосходит 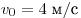 , то в точке В шайба отрывается от опоры. Длина наклонной плоскости
АВ = L = 1 м, угол α = 30°. Коэффициент трения между наклонной плоскостью и шайбой μ = 0,2. Найдите внешний радиус
трубы R. , то в точке В шайба отрывается от опоры. Длина наклонной плоскости
АВ = L = 1 м, угол α = 30°. Коэффициент трения между наклонной плоскостью и шайбой μ = 0,2. Найдите внешний радиус
трубы R.
Решение. Найдём скорость шайбы в точке B, используя закон сохранения энергии. Изменение полной механической энергии шайбы равно работе силы трения:
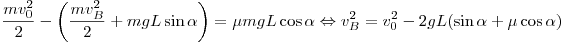 . .
Условием отрыва является равенство силы реакции опоры нулю. Центростремительное ускорение вызвано только силой тяжести, при этом
для минимальной начальной скорости, для которой наблюдается отрыв
шайбы, радиус кривизны траектории в точке B равен R (для
бо́льших скоростей радиус будет больше):
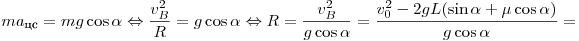
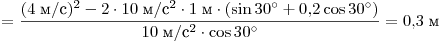 . .
Ответ: 0,3 м.
 С3. Воздушный шар, оболочка которого имеет массу
М = 145 кг и объём С3. Воздушный шар, оболочка которого имеет массу
М = 145 кг и объём 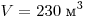 , наполняется горячим воздухом при нормальном атмосферном
давлении и температуре окружающего воздуха , наполняется горячим воздухом при нормальном атмосферном
давлении и температуре окружающего воздуха 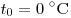 . Какую минимальную температуру t должен иметь
воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара
нерастяжима и имеет в нижней части небольшое отверстие. . Какую минимальную температуру t должен иметь
воздух внутри оболочки, чтобы шар начал подниматься? Оболочка шара
нерастяжима и имеет в нижней части небольшое отверстие.
Решение. Шар начнёт подниматься, когда сила Архимеда
превысит силу тяжести. Сила Архимеда равна 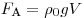 . Плотность наружного воздуха равна . Плотность наружного воздуха равна
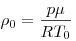 , ,
где p — нормальное атмосферное давление, μ —
молярная масса воздуха, R — газовая постоянная, 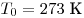 — температура наружного воздуха. — температура наружного воздуха.
Масса шара складывается из массы оболочки и массы воздуха внутри
оболочки. Сила тяжести равна
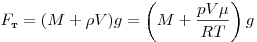 , ,
где T — температура воздух внутри оболочки.
Решая неравенство 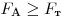 , находим
минимальную температуру T: , находим
минимальную температуру T:
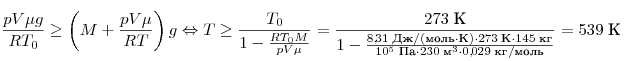 . .
Минимальная температура воздух внутри оболочки должна быть 539 К или 266 °C.
Ответ: 266 °C.
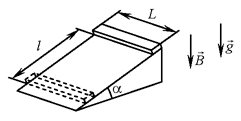 С4. Тонкий алюминиевый брусок прямоугольного сечения,
имеющий длину L = 0,5 м, соскальзывает из
состояния покоя по гладкой наклонной плоскости из диэлектрика в
вертикальном магнитном поле с индукцией
B = 0,1 Тл (см. рисунок). Плоскость наклонена к
горизонту под углом α = 30°. Продольная ось бруска
при движении сохраняет горизонтальное направление. Найдите величину ЭДС
индукции на концах бруска в момент, когда брусок пройдёт по наклонной
плоскости расстояние l = 1,6 м. С4. Тонкий алюминиевый брусок прямоугольного сечения,
имеющий длину L = 0,5 м, соскальзывает из
состояния покоя по гладкой наклонной плоскости из диэлектрика в
вертикальном магнитном поле с индукцией
B = 0,1 Тл (см. рисунок). Плоскость наклонена к
горизонту под углом α = 30°. Продольная ось бруска
при движении сохраняет горизонтальное направление. Найдите величину ЭДС
индукции на концах бруска в момент, когда брусок пройдёт по наклонной
плоскости расстояние l = 1,6 м.
Решение. Найдём скорость бруска в нижнем положении, используя закон сохранения энергии:
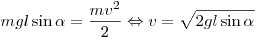 . .
Алюминий является проводником, поэтому в бруске возникнет ЭДС индукции. ЭДС индукции на концах бруска будет равно
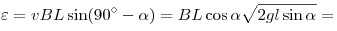
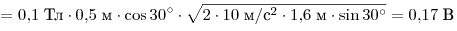 . .
Ответ: 0,17 В.
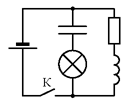 С5. В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В, ёмкость конденсатора 2 мФ,
индуктивность катушки 5 мГн, сопротивление лампы 5 Ом и
сопротивление резистора 3 Ом. В начальный момент времени ключ К
замкнут. Какая энергия выделится в лампе после размыкания ключа?
Внутренним сопротивлением источника тока, а также сопротивлением
катушки и проводов пренебречь. С5. В электрической цепи, показанной на рисунке, ЭДС источника тока равна 12 В, ёмкость конденсатора 2 мФ,
индуктивность катушки 5 мГн, сопротивление лампы 5 Ом и
сопротивление резистора 3 Ом. В начальный момент времени ключ К
замкнут. Какая энергия выделится в лампе после размыкания ключа?
Внутренним сопротивлением источника тока, а также сопротивлением
катушки и проводов пренебречь.
Решение. Введём обозначения: ε — ЭДС источника
тока, C — ёмкость конденсатора, L —
индуктивность катушки, r — сопротивление лампы, R
— сопротивление резистора.
Пока ключ замкнут через конденсатор и лампу ток не течёт, а через резистор и катушку течёт ток
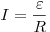 . .
Энергия системы конденсатор — лампа — катушка —
резистор равна
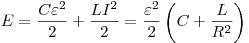 . .
После размыкания ключа в системе будут протекать переходные процессы,
пока конденсатор не разрядится и ток не станет равным нулю. Вся энергия
выделится в виде тепла в лампе и резисторе. В каждый момент времени в
лампе выделяется количества тепла 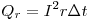 , а в
резисторе — , а в
резисторе — 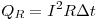 . Поскольку через
лампу и резистор будет течь один и тот же ток, отношение выделившегося
тепла будет в пропорции сопротивлений . Поскольку через
лампу и резистор будет течь один и тот же ток, отношение выделившегося
тепла будет в пропорции сопротивлений 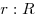 .
Таким образом, в лампе выделится энергия .
Таким образом, в лампе выделится энергия
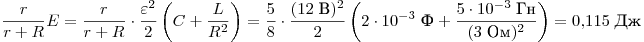
Ответ: 0,115 Дж.
С6. 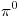 -мезон массой -мезон массой 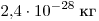 распадается на два γ-кванта.
Найдите модуль импульса одного из образовавшихся γ-квантов в
системе отсчёта, где первичный распадается на два γ-кванта.
Найдите модуль импульса одного из образовавшихся γ-квантов в
системе отсчёта, где первичный 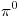 -мезон
покоится. -мезон
покоится.
Решение. В системе отсчёта, где первичный 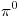 -мезон покоится, его импульс равен нулю, а энергия равна энергии покоя -мезон покоится, его импульс равен нулю, а энергия равна энергии покоя 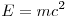 . По закону сохранения импульса γ-кванты
разлетятся в противоположных направлениях с одинаковыми импульсами.
Значит, энергии γ-квантов одинаковы и, следовательно, равны
половине энергии . По закону сохранения импульса γ-кванты
разлетятся в противоположных направлениях с одинаковыми импульсами.
Значит, энергии γ-квантов одинаковы и, следовательно, равны
половине энергии 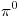 -мезона: -мезона: 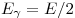 . Тогда импульс γ-кванта равен . Тогда импульс γ-кванта равен
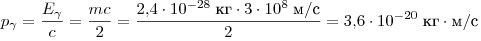 . .
Ответ: 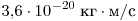 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
