|
Единый государственный экзамен по физике, 2007 год
демонстрационная версия
Скачать pdf-файл.
Часть A
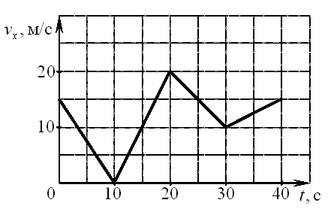 A1. Автомобиль движется по прямой улице. На графике
представлена зависимость скорости автомобиля от времени. Модуль
ускорения максимален в интервале времени A1. Автомобиль движется по прямой улице. На графике
представлена зависимость скорости автомобиля от времени. Модуль
ускорения максимален в интервале времени
|
1)
|
от 0 с до 10 с
| |
2)
|
от 10 с до 20 с
| |
3)
|
от 20 с до 30 с
| |
4)
|
от 30 с до 40 с
|
Решение. Из графика видно,
что в каждом интервале времени автомобиль двигался с постоянным
ускорениям, из которых максимальное, равное
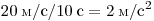 ,
было от 10 с до 20 с. ,
было от 10 с до 20 с.
Правильный ответ: 2.
А2. Две материальные точки движутся по окружностям радиусами
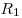 и и 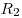 , причём , причём 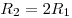 . При
условии равенства линейных скоростей точек их центростремительные
ускорения связаны соотношением . При
условии равенства линейных скоростей точек их центростремительные
ускорения связаны соотношением
Решение. При равных
линейных скоростях центростремительное ускорение обратно
пропорционально радиусу окружности. Поскольку 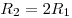 ,
значит, ,
значит, 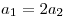 . .
Правильный ответ: 1.
А3. Парашютист спускается вертикально с постоянной скоростью
2 м/с. Систему отсчёта, связанную с Землёй, считать инерциальной.
В этом случае
|
1)
|
вес парашютиста равен нулю
| |
2)
|
сила тяжести, действующая на парашютиста, равна нулю
| |
3)
|
сумма всех сил, приложенных к парашютисту, равна нулю
| |
4)
|
сумма всех сил, действующих на парашютиста, постоянна и не равна нулю
|
Решение. Поскольку
парашютист движется с постоянной скоростью в инерциальной системе
отсчёта, то по первому закону Ньютона сумма всех сил, приложенных к
парашютисту, равна нулю.
Правильный ответ: 3.
А4. Для измерения жесткости пружины ученик собрал установку
(рис. 1), и подвесил к пружине груз массой 0,1 кг
(рис. 2). Какова жёсткость пружины?

|
1)
|
40 Н/м
| |
2)
|
20 Н/м
| |
3)
|
13 Н/м
| |
4)
|
0,05 Н/м
|
Решение. Удлинение пружины
составило 7,5 см – 2,5 см = 5 см.
Жёсткость пружины равна
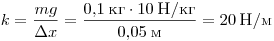 . .
Правильный ответ: 2.
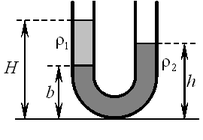 А5. В широкую U-образную трубку с вертикальными прямыми
коленами налиты неизвестная жидкость плотностью А5. В широкую U-образную трубку с вертикальными прямыми
коленами налиты неизвестная жидкость плотностью 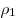 и
вода плотностью и
вода плотностью 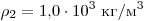 (см. рис.). На рисунке
b = 10 см, h = 24 см,
H = 30 см. Плотность жидкости (см. рис.). На рисунке
b = 10 см, h = 24 см,
H = 30 см. Плотность жидкости 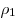 равна
равна
Решение. Плотность жидкости
можно определить из равенства давлений на одной высоте внутри жидкости:
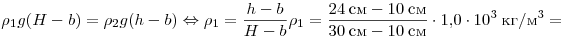
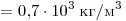 . .
Правильный ответ: 2.
А6. Два автомобиля одинаковой массы m движутся со скоростями v и 2v относительно Земли по одной прямой в противоположных направлениях. Чему равен модуль импульса второго
автомобиля в системе отсчёта, связанной с первым автомобилем?
Решение. Скорость второго
автомобиля в системе отсчёта, связанной с первым автомобилем, равна
3v, следовательно, импульс равен 3mv.
Правильный ответ: 1.
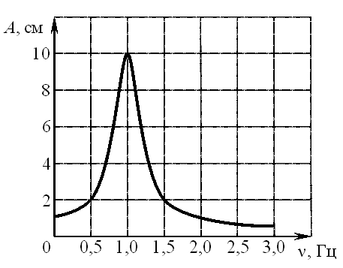 A7. На рисунке изображена зависимость амплитуды установившихся колебаний маятника от частоты вынуждающей силы (резонансная кривая). Отношение амплитуды установившихся колебаний маятника на резонансной частоте к амплитуде колебаний на частоте 0,5 Гц равно A7. На рисунке изображена зависимость амплитуды установившихся колебаний маятника от частоты вынуждающей силы (резонансная кривая). Отношение амплитуды установившихся колебаний маятника на резонансной частоте к амплитуде колебаний на частоте 0,5 Гц равно
Решение. Из графика видно,
что на частоте 0,5 Гц амплитуда равна 2 см, а на резонансно
частоте — 10 см. Отношение амплитуд равно 5.
Правильный ответ: 3.
А8. Брусок массой 0,5 кг прижат к вертикальной стене силой 10 H, направленной горизонтально. Коэффициент трения скольжения
между бруском и стеной равен 0,4. Какую минимальную силу надо приложить
к бруску по вертикали, чтобы равномерно поднимать его вертикально
вверх?
|
1)
|
9 Н
| |
2)
|
7 Н
| |
3)
|
5 Н
| |
4)
|
4 Н
|
Решение. Чтобы двигать
брусок вверх с постоянной скоростью, нужно приложенной силой
компенсировать силу тяжести и силу трения:
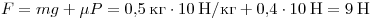 . .
Правильный ответ: 1.
А9. Скорость брошенного мяча непосредственно перед ударом о
стену была вдвое больше его скорости сразу после удара. При ударе
выделилось количество теплоты, равное 15 Дж. Найдите кинетическую
энергию мяча перед ударом.
|
1)
|
5 Дж
| |
2)
|
15 Дж
| |
3)
|
20 Дж
| |
4)
|
30 Дж
|
Решение. При уменьшении
скорости вдвое кинетическая энергия уменьшается в 4 раза. Значит,
15 Дж теплоты составляют 3/4 первоначальной кинетической энергии,
которая, тем самым, равна 20 Дж.
Правильный ответ: 3.
А10. 3 моль водорода находятся в сосуде при температуре
Т. Какова температура 3 моль кислорода в сосуде того же объёма и
при том же давлении? (Водород и кислород считать идеальными газами.)
Решение. Поскольку и объём,
и давление, и количества вещества газов одинаковые, то их температуры
также одинаковы.
Правильный ответ: 4.
А11. Внутренняя энергия газа в запаянном несжимаемом сосуде
определяется главным образом
|
1)
|
движением сосуда с газом
| |
2)
|
хаотическим движением молекул газа
| |
3)
|
взаимодействием молекул газа с Землей
| |
4)
|
действием внешних сил на сосуд с газом
|
Решение. Внутренняя энергия
газа в запаянном несжимаемом сосуде определяется главным образом
хаотическим движением молекул газа.
Правильный ответ: 2.
А12. При одинаковой температуре 100 °С
давление насыщенных паров воды равно 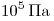 , аммиака
— , аммиака
— 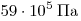 и ртути — 37 Па.
В каком из вариантов ответа эти вещества расположены в порядке убывания
температуры их кипения в открытом сосуде? и ртути — 37 Па.
В каком из вариантов ответа эти вещества расположены в порядке убывания
температуры их кипения в открытом сосуде?
|
1)
|
вода → аммиак → ртуть
| |
2)
|
аммиак → ртуть → вода
| |
3)
|
вода → ртуть → аммиак
| |
4)
|
ртуть → вода → аммиак
|
Решение. Давление
насыщенных паров воды равно атмосферному, поэтому температура её
кипения равна 100 °С. Давление насыщенных паров
аммиака выше атмосферного, следовательно, температура его кипения
меньше 100 °С. Давление насыщенных паров ртути меньше
атмосферного, значит, температура её кипения больше
100 °С. Таким образом, вещества расположены в
следующем порядке убывания температуры их кипения в открытом сосуде:
ртуть → вода → аммиак.
Правильный ответ: 4.
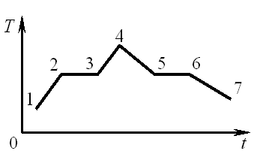 A13. На графике (см. рис.) представлено изменение температуры T вещества с течением времени t. В начальный момент времени вещество находилось в кристаллическом состоянии. Какая из точек соответствует окончанию процесса отвердевания? A13. На графике (см. рис.) представлено изменение температуры T вещества с течением времени t. В начальный момент времени вещество находилось в кристаллическом состоянии. Какая из точек соответствует окончанию процесса отвердевания?
Решение. Точка 1 на графике
соответствует кристаллическому состоянию вещества. Точки 2, 3, 5, 6
— переходу между кристаллическим состоянием и жидким, причём
точка 6 соответствует окончанию процесса отвердевания?
Правильный ответ: 2.
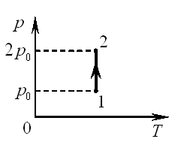 A14. На диаграмме (см. рис.) показан процесс изменения
состояния идеального одноатомного газа. Газ отдаёт 50 кДж теплоты.
Работа внешних сил равна A14. На диаграмме (см. рис.) показан процесс изменения
состояния идеального одноатомного газа. Газ отдаёт 50 кДж теплоты.
Работа внешних сил равна
|
1)
|
0 кДж
| |
2)
|
25 кДж
| |
3)
|
50 кДж
| |
4)
|
100 кДж
|
Решение. В изотермическом
процессе изменение внутренней энергии равно нулю, а работа внешних сил
равна отданной газом теплоте, т. е. 50 кДж.
Правильный ответ: 3.
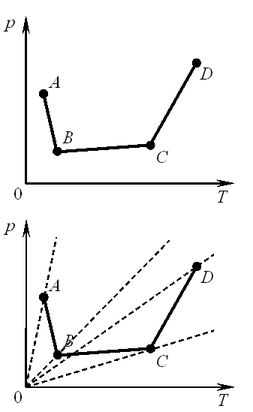 A15. В сосуде постоянного объёма находится идеальный газ, массу которого изменяют. На диаграмме (см. рис.) показан процесс
изменения состояния газа. В какой из точек диаграммы масса газа
наибольшая? A15. В сосуде постоянного объёма находится идеальный газ, массу которого изменяют. На диаграмме (см. рис.) показан процесс
изменения состояния газа. В какой из точек диаграммы масса газа
наибольшая?
Решение. Проведём на
графике линии, соответствующие постоянной массе и проходящие через
точки A, B, C и D (см. рис.). Чем
больше угол наклона линии, тем больше масса газа. Таким образом,
наибольшая масса газа в состоянии A.
Правильный ответ: 1.
А16. Пылинка, имевшая отрицательный заряд –10е, при освещении потеряла четыре электрона. Каким стал заряд пылинки?
|
1)
|
6e
| |
2)
|
–6e
| |
3)
|
14e
| |
4)
|
–14e
|
Решение. При потере четырёх
электронов заряд пылинки увеличился на 4e и стал
–6e.
Правильный ответ: 2.
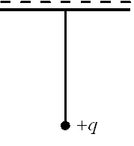 A17. К бесконечной горизонтальной отрицательно заряженной
плоскости привязана невесомая нить с шариком, имеющим положительный
заряд (см. рис.). Каково условие равновесия шарика, если mg — модуль силы тяжести, A17. К бесконечной горизонтальной отрицательно заряженной
плоскости привязана невесомая нить с шариком, имеющим положительный
заряд (см. рис.). Каково условие равновесия шарика, если mg — модуль силы тяжести, 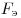 — модуль силы электростатического взаимодействия шарика с пластиной, T — модуль силы натяжения нити? — модуль силы электростатического взаимодействия шарика с пластиной, T — модуль силы натяжения нити?
Решение. Сила тяжести
направлена вниз, сила электростатического взаимодействия шарика с
пластиной и сила натяжения нити — вверх. В равновесии сумма сил
равна нулю:
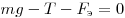 . .
Правильный ответ: 4.
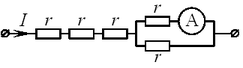 A18. Через участок цепи (см. рис.) течёт постоянный ток
I = 10 А. Какую силу тока показывает амперметр? Сопротивлением амперметра пренебречь. A18. Через участок цепи (см. рис.) течёт постоянный ток
I = 10 А. Какую силу тока показывает амперметр? Сопротивлением амперметра пренебречь.
|
1)
|
2 А
| |
2)
|
3 А
| |
3)
|
5 А
| |
4)
|
10 А
|
Решение. Поскольку
сопротивления резисторов, расположенных в параллельных участках цепи,
равны, сила тока в каждом из них будет вдвое меньше силы тока в
основной цепи. Амперметр показывает силу тока 5 А.
Правильный ответ: 3.
А19. В электронагревателе, через который течёт постоянный ток,
за время t выделяется количество теплоты Q. Если
сопротивление нагревателя и время t увеличить вдвое, не изменяя
силу тока, то количество выделившейся теплоты будет равно
Решение. При постоянной
силе тока, выделяющаяся теплота прямо пропорциональна сопротивлению
нагревателя и времени его работы. При увеличении их вдвое выделяющаяся
теплота увеличивается в 4 раза.
Правильный ответ: 2.
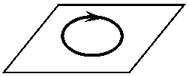 A20. На рисунке изображён проволочный виток, по которому течёт
электрический ток в направлении, указанном стрелкой. Виток расположен в
горизонтальной плоскости. В центре витка вектор индукции магнитного
поля тока направлен A20. На рисунке изображён проволочный виток, по которому течёт
электрический ток в направлении, указанном стрелкой. Виток расположен в
горизонтальной плоскости. В центре витка вектор индукции магнитного
поля тока направлен
|
1)
|
вертикально вверх 
| |
2)
|
горизонтально влево 
| |
3)
|
горизонтально вправо 
| |
4)
|
вертикально вниз 
|
Решение. Направление вектор
индукции магнитного поля можно определить по правилу правого винта.
Если правый винт крутить в направлении, указанном на рисунке, он будет
двигаться вертикально вниз. Туда же направлен вектор индукции
магнитного поля.
Правильный ответ: 4.
А21. Инфракрасное излучение испускают
|
1)
|
электроны при их направленном движении в проводнике
| |
2)
|
атомные ядра при их превращениях
| |
3)
|
любые заряженные частицы
| |
4)
|
любые нагретые тела
|
Решение. Инфракрасное
излучение испускают нагретые тела.
Правильный ответ: 4.
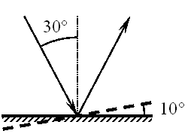 A22. Угол падения света на горизонтально расположенное плоское зеркало равен 30°. Каким будет угол между падающим и
отражённым лучами, если повернуть зеркало на 10° так, как
показано на рисунке? A22. Угол падения света на горизонтально расположенное плоское зеркало равен 30°. Каким будет угол между падающим и
отражённым лучами, если повернуть зеркало на 10° так, как
показано на рисунке?
|
1)
|
80°
| |
2)
|
60°
| |
3)
|
40°
| |
4)
|
20°
|
Решение. После поворота
зеркала на 10° угол падения составит 20°, а
угол между падающим и отражённым лучами — 40°.
Правильный ответ: 3.
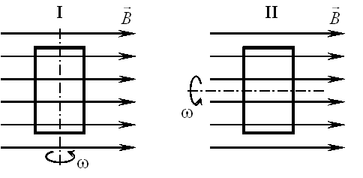 A23. На рисунке показаны два способа вращения рамки в
однородном магнитном поле. Ток в рамке A23. На рисунке показаны два способа вращения рамки в
однородном магнитном поле. Ток в рамке
|
1)
|
возникает в обоих случаях
| |
2)
|
не возникает ни в одном из случаев
| |
3)
|
возникает только в первом случае
| |
4)
|
возникает только во втором случае
|
Решение. При вращении рамки
первым способом пронизывающий её магнитный поток будет постоянно
изменяться, ток в рамке возникнет. При вращении рамки по второму
способу пронизывающий её магнитный поток будет постоянно оставаться
равным нулю, ток в рамке не возникнет.
Правильный ответ: 3.
А24. На рисунке представлен график изменения заряда
конденсатора в колебательном контуре с течением времени.
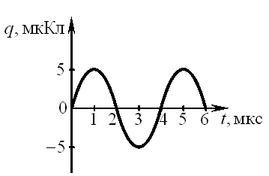
На каком из графиков правильно показан процесс изменения силы тока с течением времени в этом колебательном контуре?
Решение. Поскольку заряд
конденсатора изменяется по синусоидальному закону, сила тока также
будет меняться по синусоидальному закону со сдвигом фазы на четверть
периода.
Правильный ответ: 2.
А25. Энергия фотона, поглощаемого атомом при переходе из
основного состояния с энергией 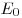 в возбужденное состояние
с энергией в возбужденное состояние
с энергией 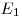 , равна , равна
Решение. Энергия фотона
равна  . .
Правильный ответ: 1.
 A26. На рисунках А, Б, В приведены спектры излучения паров стронция, неизвестного образца и кальция. Можно
утверждать, что в образце A26. На рисунках А, Б, В приведены спектры излучения паров стронция, неизвестного образца и кальция. Можно
утверждать, что в образце
|
1)
|
не содержится ни стронция, ни кальция
| |
2)
|
содержится кальций, но нет стронция
| |
3)
|
содержатся и стронций, и кальций
| |
4)
|
содержится стронций, но нет кальция
|
Решение. В спектре
неизвестного образца есть все линии спектра стронция и не
все линии спектра кальция, значит, неизвестный образец содержится
стронций, но нет кальция.
Правильный ответ: 4.
А27. Какая из строчек таблицы правильно отражает структуру ядра  ? ?
| |
p — число протонов
|
n — число протонов
|
|
1)
|
48
|
68
|
|
2)
|
28
|
20
|
|
3)
|
20
|
48
|
|
4)
|
20
|
28
|
Решение. Число протонов
ядра  указано нижним
индексом, т. е. равно 20. Число нейтронов равно разности верхнего
и нижнего индекса записи, т. е. равно 48 – 20 = 28. указано нижним
индексом, т. е. равно 20. Число нейтронов равно разности верхнего
и нижнего индекса записи, т. е. равно 48 – 20 = 28.
Правильный ответ: 4.
А28. Полоний 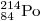 превращается в висмут превращается в висмут 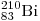 в результате радиоактивных распадов: в результате радиоактивных распадов:
|
1)
|
одного α и одного β
| |
2)
|
одного α и двух β
| |
3)
|
двух α и одного β
| |
4)
|
двух α и двух β
|
Решение. При α-распаде
масса ядра уменьшается на 4 а. е. м., а при
β-распаде масса не изменяется. В серии распадов масса ядра
уменьшилась на
214 – 210 = 4 а. е. м. Для
такого уменьшения массы требуется один α-распад. При
α-распаде заряд ядра уменьшается на 2, а при β-распаде
— увеличивается на 1. В серии распадов заряд ядра уменьшился на
1. Для такого уменьшения заряда кроме один α-распада требуется
один β-распад.
Правильный ответ: 1.
А29. Красная граница фотоэффекта исследуемого металла
соответствует длине волны 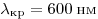 . При
освещении этого металла светом длиной волны λ максимальная
кинетическая энергия выбитых из него фотоэлектронов в 3 раза меньше
энергии падающего света. Какова длина волны λ падающего света? . При
освещении этого металла светом длиной волны λ максимальная
кинетическая энергия выбитых из него фотоэлектронов в 3 раза меньше
энергии падающего света. Какова длина волны λ падающего света?
|
1)
|
133 нм
| |
2)
|
300 нм
| |
3)
|
400 нм
| |
4)
|
1200 нм
|
Решение. По условию задачи:
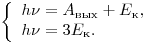
Учитывая, что 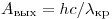 , получаем: , получаем:
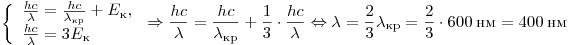 . .
Правильный ответ: 3.
А30. В лаборатории исследовалась зависимость напряжения на обкладках конденсатора от заряда этого конденсатора. Результаты измерений представлены в таблице.
|
q, мкКл
|
0,1
|
0,2
|
0,3
|
0,4
|
0,5
|
|
U, кВ
|
0,5
|
1,5
|
3,0
|
3,5
|
3,8
|
Погрешности измерений величин q и U равнялись
соответственно 0,05 мкКл и 0,25 кВ. Какой из графиков
приведён правильно с учётом всех результатов измерения и погрешностей
этих измерений?
Решение. Нанесём результаты
измерения с погрешностями на график (см. рис.). Видно, что как
первый, так и второй графики могут считаться правильно проведёнными.
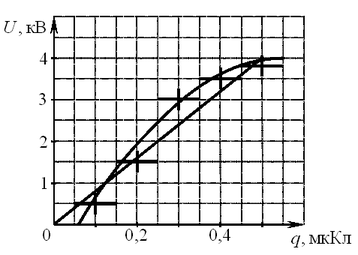
Правильный ответ: 1 и 2.
Примечание. При отсутствии
веских причин среди всех линий, которые можно провести через результаты
измерений, выбирают кривую с наименьшим числом перегибов (а из кривой и
прямой — прямую линию). Кроме того, в идеальном конденсаторе его
заряд и напряжение на обкладках прямо пропорциональны. Составители
считают верным второй вариант ответа.
Часть B
В1. Небольшой камень, брошенный с ровной горизонтальной
поверхности земли под углом к горизонту, упал обратно на землю в
20 м от места броска. Чему была равна скорость камня через 1 с
после броска, если в этот момент она была направлена горизонтально?
Решение. Скорость камня
горизонтальна в наивысшей точке полёта. Значит, время подъёма и время
падения равны 1 с. За 2 с камень преодолел 20 м по
горизонтали, следовательно, составляющая его скорости, направленная
вдоль горизонта, равна 10 м/с. В верхней точке полёта полная
скорость совпадает со своей горизонтальной проекцией.
Ответ: 10.
В2. 1 моль инертного газа сжали, совершив работу 600 Дж. В
результате сжатия температура газа повысилась на
40 °С. Какое количество теплоты отдал газ? Ответ
округлите до целых.
Решение. Используя первое
начало термодинамики, получаем:
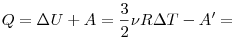
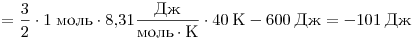 . .
Газ отдал 101 Дж теплоты.
Ответ: 101.
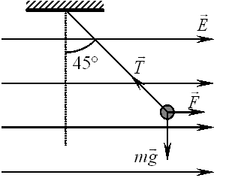 B3. В электрическом поле, вектор напряженности которого
направлен горизонтально и равен по модулю 1000 В/м, нить с
подвешенным на ней маленьким заряженным шариком отклонилась на угол
45° от вертикали. Масса шарика 1,4 г. Чему равен заряд
шарика? Ответ выразите в микрокулонах (мкКл) и округлите до целых. B3. В электрическом поле, вектор напряженности которого
направлен горизонтально и равен по модулю 1000 В/м, нить с
подвешенным на ней маленьким заряженным шариком отклонилась на угол
45° от вертикали. Масса шарика 1,4 г. Чему равен заряд
шарика? Ответ выразите в микрокулонах (мкКл) и округлите до целых.
Решение. На шарик действуют
три силы (см. рис.): сила тяжести, сила натяжения нити и сила со
стороны электрического поля. В равновесии сумма этих сил равна нулю:
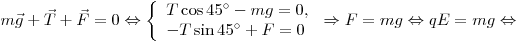
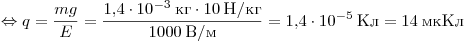 . .
Ответ: 14.
В4. На дифракционную решетку, имеющую период 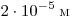 , падает нормально параллельный пучок белого света. Спектр наблюдается на экране на расстоянии 2 м от решетки. Каково
расстояние между красным и фиолетовым участками спектра первого порядка
(первой цветной полоски на экране), если длины волн красного и
фиолетового света соответственно равны , падает нормально параллельный пучок белого света. Спектр наблюдается на экране на расстоянии 2 м от решетки. Каково
расстояние между красным и фиолетовым участками спектра первого порядка
(первой цветной полоски на экране), если длины волн красного и
фиолетового света соответственно равны 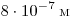 и и 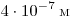 ? Считать ? Считать
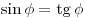 . Ответ выразите в см. . Ответ выразите в см.
Решение. Углы отклонения
связаны с постоянной решётки и длиной волны света равенством 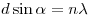 . Тогда для красного и фиолетового лучей
имеем: . Тогда для красного и фиолетового лучей
имеем:
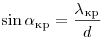 , , 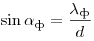 . .
Отклонение составит 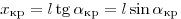 и и  . Таким образом, расстояние между красным и фиолетовым участками спектра первого порядка равно . Таким образом, расстояние между красным и фиолетовым участками спектра первого порядка равно
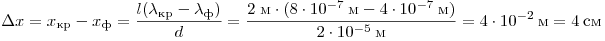
Ответ: 4.
Часть C
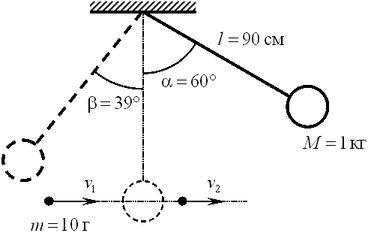 C1. Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60° и
отпускают. В момент прохождения шаром положения равновесия в него
попадает пуля массой 10 г, летящая навстречу шару. Она пробивает
его и продолжает двигаться горизонтально. Определите изменение скорости
пули в результате попадания в шар, если он, продолжая движение в
прежнем направлении, отклоняется на угол 39°. (Массу шара
считать неизменной, диаметр шара — пренебрежимо малым по
сравнению с длиной нити, C1. Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60° и
отпускают. В момент прохождения шаром положения равновесия в него
попадает пуля массой 10 г, летящая навстречу шару. Она пробивает
его и продолжает двигаться горизонтально. Определите изменение скорости
пули в результате попадания в шар, если он, продолжая движение в
прежнем направлении, отклоняется на угол 39°. (Массу шара
считать неизменной, диаметр шара — пренебрежимо малым по
сравнению с длиной нити, 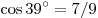 .) .)
Решение. Скорость шара
в нижней точке до столкновения с пулей равна 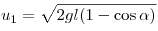 , а после столкновения , а после столкновения 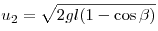 . Эти скорости направлены горизонтально навстречу
движения пули. Используя закон сохранения импульса, находим изменение
скорости пули: . Эти скорости направлены горизонтально навстречу
движения пули. Используя закон сохранения импульса, находим изменение
скорости пули:
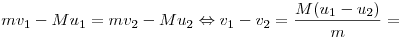
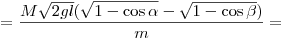
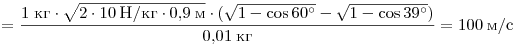 . .
Ответ: 100 м/с.
С2. Воздушный шар с газонепроницаемой оболочкой массой
400 кг заполнен гелием. На высоте, где температура воздуха
17 °С и давление 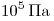 , шар может
удерживать груз массой 225 кг. Какова масса гелия в оболочке шара?
Считать, что оболочка шара не оказывает сопротивления изменению объёма
шара. , шар может
удерживать груз массой 225 кг. Какова масса гелия в оболочке шара?
Считать, что оболочка шара не оказывает сопротивления изменению объёма
шара.
Решение. На воздушный шар
действуют сила тяжести и выталкивающая сила. В равновесии они
уравновешивают друг друга:
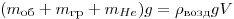 , ,
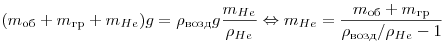 . .
Плотности воздуха и гелия можно определить, используя уравнения
Менделеева — Клапейрона:
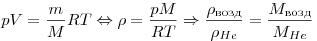 . .
Таким образом, получаем:
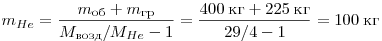 . .
Ответ: 100 кг.
С3. К однородному медному цилиндрическому проводнику длиной
10 м приложили разность потенциалов 1 В. Определите
промежуток времени, в течение которого температура проводника повысится
на 10 К. Изменением сопротивления проводника и рассеянием тепла
при его нагревании пренебречь. (Удельное сопротивление меди
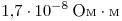 .) .)
Решение. Обозначим
длину проводника 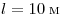 , площадь его сечения
S, плотность , площадь его сечения
S, плотность 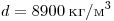 , удельное
сопротивление , удельное
сопротивление 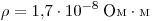 , теплоёмкость , теплоёмкость 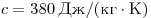 . Сопротивление проводника равно . Сопротивление проводника равно 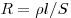 . За время t в нём выделится . За время t в нём выделится 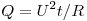 теплоты, при этом он нагреется на теплоты, при этом он нагреется на 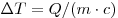 градусов, где градусов, где 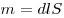 — масса проводника. В итоге получаем — масса проводника. В итоге получаем
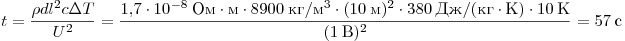 . .
Ответ: 57 с.
С4. В дно водоема глубиной 3 м вертикально вбита свая,
скрытая под водой. Высота сваи 2 м. Свая отбрасывает на дне
водоема тень длиной 0,75 м. Определите угол падения солнечных
лучей на поверхность воды. Показатель преломления воды
n = 4/3.
Решение. Угол падения
(α) связан с углом преломления (β) соотношением:
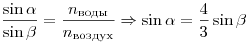 . .
По длине тени можно определить угол преломления:
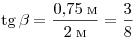 . .
В итоге получаем:
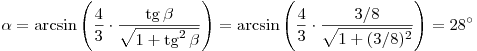 . .
Ответ: 28°.
С5. Фотокатод, покрытый кальцием (работа выхода
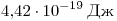 ), освещается светом с длиной волны 300 нм. Вылетевшие из катода электроны попадают в однородное магнитное поле с индукцией ), освещается светом с длиной волны 300 нм. Вылетевшие из катода электроны попадают в однородное магнитное поле с индукцией 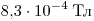 перпендикулярно линиям индукции этого поля. Каков максимальный радиус окружности, по которой движутся электроны? перпендикулярно линиям индукции этого поля. Каков максимальный радиус окружности, по которой движутся электроны?
Решение. Используя уравнение Эйнштейна для фотоэффекта, находим максимальный импульс фотоэлектронов:
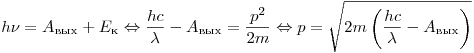 . .
Максимальный радиус равен
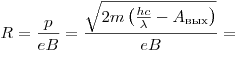
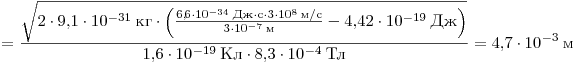 . .
Ответ: 4,7 мм.
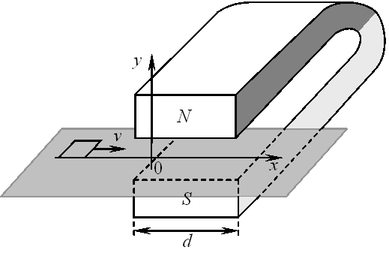 C6. Квадратная рамка со стороной b = 5 см
изготовлена из медной проволоки сопротивлением R = 0,1 Ом. Рамку перемещают по гладкой горизонтальной поверхности с постоянной скоростью v вдоль оси 0x. Начальное положение рамки изображено на рисунке. За время движения рамка проходит между полюсами магнита и вновь оказывается в области, где магнитное поле отсутствует. Индукционные токи, возникающие в рамке, оказывают тормозящее действие, поэтому для поддержания постоянной скорости движения к ней прикладывают внешнюю силу F, направленную вдоль оси 0x. С какой скоростью движется рамка, если суммарная работа внешней силы за время движения равна C6. Квадратная рамка со стороной b = 5 см
изготовлена из медной проволоки сопротивлением R = 0,1 Ом. Рамку перемещают по гладкой горизонтальной поверхности с постоянной скоростью v вдоль оси 0x. Начальное положение рамки изображено на рисунке. За время движения рамка проходит между полюсами магнита и вновь оказывается в области, где магнитное поле отсутствует. Индукционные токи, возникающие в рамке, оказывают тормозящее действие, поэтому для поддержания постоянной скорости движения к ней прикладывают внешнюю силу F, направленную вдоль оси 0x. С какой скоростью движется рамка, если суммарная работа внешней силы за время движения равна 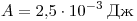 ? Ширина полюсов магнита d = 20 см, магнитное поле имеет резкую границу, однородно между полюсами, а его индукция B = 1 Тл. ? Ширина полюсов магнита d = 20 см, магнитное поле имеет резкую границу, однородно между полюсами, а его индукция B = 1 Тл.
Решение. Индукционные
токи возникают в рамке только при пересечении рамкой границы поля.
Магнитный поток меняется от 0 до 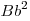 (при выходе от (при выходе от
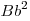 до 0) за время до 0) за время 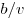 . В рамке возникает ЭДС
индукции, равная . В рамке возникает ЭДС
индукции, равная 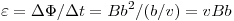 , вследствие чего в рамке течёт индукционный ток , вследствие чего в рамке течёт индукционный ток
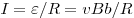 . .
Действующие силы Ампера на участки
рамки, направленные вдоль оси 0x и находящиеся в магнитном поле,
компенсируют друг друга. Действие силы Ампера, равной 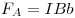 и приложенной к участку рамки, расположенной перпендикулярно
к оси 0x, компенсируется внешней силой и приложенной к участку рамки, расположенной перпендикулярно
к оси 0x, компенсируется внешней силой 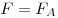 .
Работа этой силы равна .
Работа этой силы равна 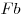 при входе рамки в магнитное поле.
Такую же работу совершает эта сила при выходе рамки из поля. В итоге
получаем: при входе рамки в магнитное поле.
Такую же работу совершает эта сила при выходе рамки из поля. В итоге
получаем:
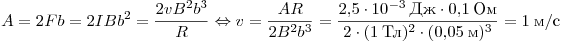 . .
Ответ: 1 м/с.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
