|
Единый государственный экзамен по физике, 2006 год
демонстрационная версия
Скачать pdf-файл.
Часть A
А1. Велосипедист съезжает с горки, двигаясь прямолинейно и равноускоренно. За время спуска скорость велосипедиста увеличилась на 10 м/с. Ускорение велосипедиста 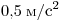 . Сколько времени длится спуск? . Сколько времени длится спуск?
|
1)
|
0,05 с
| |
2)
|
2 с
| |
3)
|
5 с
| |
4)
|
20 с
|
Решение. Время спуска равно
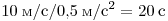 . .
Правильный ответ: 4.
А2. В инерциальной системе отсчёта движутся два
тела. Первому телу массой m сила F сообщает ускорение a. Чему равна масса второго тела, если вдвое меньшая сила сообщила ему в 4 раза бо́льшее ускорение?
Решение.
Масса может быть
рассчитана по формуле 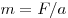 . Вдвое меньшая сила сообщает в
4 раза бо́льшее ускорение телу с массой . Вдвое меньшая сила сообщает в
4 раза бо́льшее ускорение телу с массой 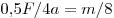 . .
Правильный ответ: 2.
А3. На какой стадии полёта в космическом
корабле, который
становится на орбите спутником Земли, будет наблюдаться невесомость?
|
1)
|
на стартовой позиции с включенным двигателем
| |
2)
|
при выходе на орбиту с включенным двигателем
| |
3)
|
при орбитальном полете с выключенным двигателем
| |
4)
|
при посадке с парашютом с выключенным двигателем
|
Решение.
Невесомость
наблюдаться в условиях отсутствия всех внешних сил, за исключением
гравитационных. В таких условиях находится космический корабль при
орбитальном полете с выключенным двигателем.
Правильный ответ: 3.
А4. Два шара массами m и 2m
движутся со
скоростями, равными соответственно 2v и v. Первый шар
движется за вторым и, догнав, прилипает к нему. Каков суммарный импульс
шаров после удара?
|
1)
|
mv
| |
2)
|
2mv
| |
3)
|
3mv
| |
4)
|
4mv
|
Решение. По
закону
сохранения суммарный импульс шаров после удара равен сумме импульсов
шаров до столкновения: 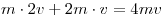 . .
Правильный ответ: 4.
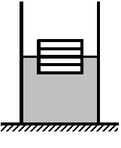 А5.
Четыре одинаковых листа фанеры толщиной L каждый,
связанные в стопку, плавают в воде так, что уровень воды соответствует
границе между двумя средними листами. Если в стопку добавить еще один
такой же лист, то глубина погружения стопки листов увеличится на А5.
Четыре одинаковых листа фанеры толщиной L каждый,
связанные в стопку, плавают в воде так, что уровень воды соответствует
границе между двумя средними листами. Если в стопку добавить еще один
такой же лист, то глубина погружения стопки листов увеличится на
Решение.
Глубина погружения
составляет половину высоты стопки: для четырёх листов —
2L, для пяти листов — 2,5L. Глубина погружения
увеличится на 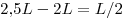 . .
Правильный ответ: 3.
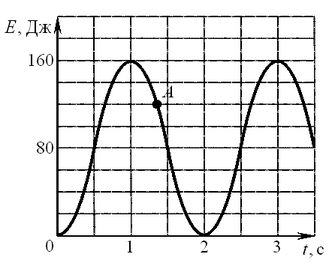
A6. На рисунке представлен график изменения со временем
кинетической энергии ребёнка, качающегося на качелях. В момент,
соответствующий точке A на графике, его потенциальная энергия,
отсчитанная от положения равновесия качелей, равна
|
1)
|
40 Дж
| |
2)
|
80 Дж
| |
3)
|
120 Дж
| |
4)
|
160 Дж
|
Решение.
Известно, что в
положении равновесия наблюдается максимум кинетической энергии, а
разность потенциальных энергий в двух состояниях равна по модулю
разности кинетических энергий. Из графика видно, что максимальная
кинетическая энергия равна 160 Дж, а для точки А она равна
120 Дж. Таким образом, потенциальная энергия, отсчитанная от
положения равновесия качелей, равна 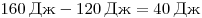 . .
Правильный ответ: 1.
А7. Две материальные точки движутся по
окружностям радиусами
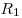 и и 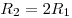 с одинаковыми по модулю
скоростями. Их периоды обращения по окружностям связаны соотношением с одинаковыми по модулю
скоростями. Их периоды обращения по окружностям связаны соотношением
Решение.
Период обращения
по окружности равен 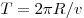 . Поскольку . Поскольку 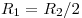 , то , то 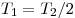 . .
Правильный ответ: 4.
А8. В жидкостях частицы совершают колебания
возле положения
равновесия, сталкиваясь с соседними частицами. Время от времени частица
совершает «прыжок» к другому положению равновесия. Какое
свойство жидкостей можно объяснить таким характером движения частиц?
|
1)
|
малую сжимаемость
| |
2)
|
текучесть
| |
3)
|
давление на дно сосуда
| |
4)
|
изменение объёма при нагревании
|
Решение. Таким характером
движения частиц жидкости объясняется её текучесть.
Правильный ответ: 2.
А9. Лёд при температуре 0 °C внесли в тёплое
помещение. Температура льда до того, как он растает,
|
1)
|
не изменится, так как вся энергия, получаемая льдом в это время,
расходуется на разрушение кристаллической решетки
| |
2)
|
не изменится, так как при плавлении лед получает тепло от окружающей
среды, а затем отдаёт его обратно
| |
3)
|
повысится, так как лёд получает тепло от окружающей среды, значит, его
внутренняя энергия растёт, и температура льда повышается
| |
4)
|
понизится, так как при плавлении лед отдаёт окружающей среде некоторое
количество теплоты
|
Решение.
Температура льда
до того, как он растает, не изменится, так как вся энергия, получаемая
льдом в это время, расходуется на разрушение кристаллической решетки.
Правильный ответ: 1.
А10. При какой влажности воздуха человек легче
переносит
высокую температуру воздуха и почему?
|
1)
|
при низкой, так как при этом пот испаряется быстро
| |
2)
|
при низкой, так как при этом пот испаряется медленно
| |
3)
|
при высокой, так как при этом пот испаряется быстро
| |
4)
|
при высокой, так как при этом пот испаряется медленно
|
Решение.
Человек легче
переносит высокую температуру воздуха при низкой влажности, так как при
этом пот испаряется быстро.
Правильный ответ: 1.
А11. Абсолютная температура тела равна 300 К. По шкале Цельсия она равна
|
1)
|
–27 °C
| |
2)
|
27 °C
| |
3)
|
300 °C
| |
4)
|
573 °C
|
Решение. По
шкале Цельсия
она равна 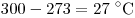 . .
Правильный ответ: 2.
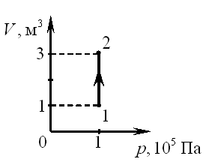 A12. На рисунке приведён график зависимости объёма идеального одноатомного газа от давления в процессе 1–2. Внутренняя энергия
газа при этом увеличилась на 300 кДж. Количество теплоты,
сообщенное газу в этом процессе, равно A12. На рисунке приведён график зависимости объёма идеального одноатомного газа от давления в процессе 1–2. Внутренняя энергия
газа при этом увеличилась на 300 кДж. Количество теплоты,
сообщенное газу в этом процессе, равно
|
1)
|
0 кДж
| |
2)
|
100 кДж
| |
3)
|
200 кДж
| |
4)
|
500 кДж
|
Решение. По первому началу
термодинамики сообщенное газу количество теплоты равно 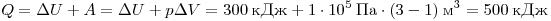 . .
Правильный ответ: 4.
А13. Тепловая машина с КПД 60 % за цикл
работы получает от
нагревателя количество теплоты, равное 100 Дж. Какую полезную работу
машина совершает за цикл?
|
1)
|
40 Дж
| |
2)
|
60 Дж
| |
3)
|
100 Дж
| |
4)
|
160 Дж
|
Решение. КПД тепловой
машины, совершаемая ею полезная работа и получаемое от нагревателя
количество теплоты связаны равенством 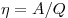 , откуда , откуда
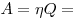 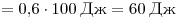 . .
Правильный ответ: 2.
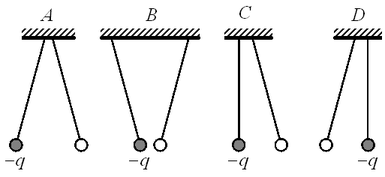 A14. Два одинаковых лёгких шарика, заряды которых равны по модулю, подвешены на шёлковых нитях. Заряд одного из шариков указан на рисунках. Какой(-ие) из рисунков соответствует(-ют) ситуации, когда
заряд 2-го шарика отрицателен? A14. Два одинаковых лёгких шарика, заряды которых равны по модулю, подвешены на шёлковых нитях. Заряд одного из шариков указан на рисунках. Какой(-ие) из рисунков соответствует(-ют) ситуации, когда
заряд 2-го шарика отрицателен?
|
1)
|
A
| |
2)
|
B
| |
3)
|
C и D
| |
4)
|
A и C
|
Решение. Указанный заряд шарика — отрицательный. Одноимённые заряды отталкиваются.
Отталкивание наблюдается на рисунке A.
Правильный ответ: 1.
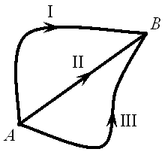 A15.
α-частица перемещается в однородном
электростатическом поле из точки A в точку B по
траекториям I, II, III (см. рис.). Работа сил электростатического
поля A15.
α-частица перемещается в однородном
электростатическом поле из точки A в точку B по
траекториям I, II, III (см. рис.). Работа сил электростатического
поля
|
1)
|
наибольшая на траектории I
| |
2)
|
наибольшая на траектории II
| |
3)
|
одинаковая только на траекториях I и III
| |
4)
|
одинаковая на траекториях I, II и III
|
Решение. Электростатическое
поле является потенциальным. В нём работа по перемещению заряда не
зависит от траектории, а зависит от положения начальной и конечной
точек. Для нарисованных траекторий начальные и конечные точки
совпадают, значит, и работы сил электростатического поля одинаковы.
Правильный ответ: 4.
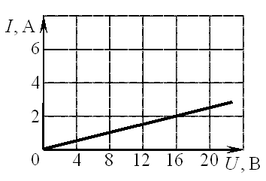 A16. На рисунке изображен график зависимости силы тока в
проводнике от напряжения на его концах. Чему равно сопротивление
проводника? A16. На рисунке изображен график зависимости силы тока в
проводнике от напряжения на его концах. Чему равно сопротивление
проводника?
|
1)
|
0,125 Ом
| |
2)
|
2 Ом
| |
3)
|
16 Ом
| |
4)
|
8 Ом
|
Решение.
Сопротивление
может быть рассчитано по формуле 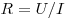 . Из графика видно,
что . Из графика видно,
что 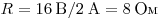 . .
Правильный ответ: 4.
А17. Какими носителями электрического заряда
создаётся ток в
водном растворе соли?
|
1)
|
только ионами
| |
2)
|
электронами и «дырками»
| |
3)
|
электронами и ионами
| |
4)
|
только электронами
|
Решение. В водном растворе соли ток создаётся только ионами.
Правильный ответ: 1.
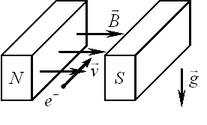 А18. Электрон А18. Электрон  , влетевший в зазор между
полюсами электромагнита, имеет горизонтально направленную скорость , влетевший в зазор между
полюсами электромагнита, имеет горизонтально направленную скорость
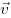 , перпендикулярную вектору индукции магнитного поля , перпендикулярную вектору индукции магнитного поля
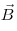 (см. рис.). Куда направлена действующая на
электрон сила Лоренца? (см. рис.). Куда направлена действующая на
электрон сила Лоренца?
|
1)
|
вертикально вниз
| |
2)
|
вертикально вверх
| |
3)
|
горизонтально влево
| |
4)
|
горизонтально вправо
|
Решение. Воспользуемся
правилом «левой руки»: направим четыре пальца руки в
сторону направления движения электрона (от себя), а ладонь развернём
так, чтобы линии магнитного поля входили в неё (влево). Тогда
оттопыренный большой палец покажет направление действующей силы (он
будет направлен вниз), если бы частица была заряжена положительно.
Заряд электрона отрицательный, значит, сила Лоренца будет направлена в
противоположную сторону: вертикально вверх.
Правильный ответ: 2.
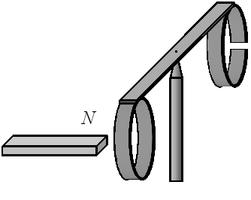 A19. На рисунке приведена демонстрация опыта по проверке
правила Ленца. Опыт проводится со сплошным кольцом, а не разрезанным,
потому что A19. На рисунке приведена демонстрация опыта по проверке
правила Ленца. Опыт проводится со сплошным кольцом, а не разрезанным,
потому что
|
1)
|
сплошное кольцо сделано из стали, а разрезанное — из алюминия
| |
2)
|
в сплошном кольце не возникает вихревое электрическое поле, а в
разрезанном — возникает
| |
3)
|
в сплошном кольце возникает индукционный ток, а в разрезанном —
нет
| |
4)
|
в сплошном кольце возникает ЭДС индукции, а в разрезанном — нет
|
Решение.
Опыт проводится со
сплошным кольцом, потому что в сплошном кольце возникает индукционный
ток, а в разрезанном — нет.
Правильный ответ: 3.
А20. Разложение белого света в спектр при прохождении через призму обусловлено:
|
1)
|
интерференцией света
| |
2)
|
дисперсией света
| |
3)
|
отражением света
| |
4)
|
дифракцией света
|
Решение. Разложение белого
света в спектр при прохождении через призму обусловлено дисперсией
света.
Правильный ответ: 2.
А21. Объектив фотоаппарата — собирающая линза с фокусным расстоянием F = 50 мм. При фотографировании
предмета, удалённого от фотоаппарата на 40 см, изображение
предмета получается чётким, если плоскость фотоплёнки находится от
объектива на расстоянии
|
1)
|
бо́льшем, чем 2F
| |
2)
|
равном 2F
| |
3)
|
между F и 2F
| |
4)
|
равном F
|
Решение. Используя формулу
для линзы, определим положение изображения предмета:
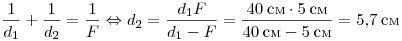 . .
Если на этом расстоянии расположить плоскость фотоплёнки, то получится чёткое изображение. Видно, что 50 мм < 57 мм < 100 мм.
Правильный ответ: 3.
А22. Скорость света во всех инерциальных
системах отсчёта
|
1)
|
не зависит ни от скорости приёмника света, ни от скорости источника
света
| |
2)
|
зависит только от скорости движения источника света
| |
3)
|
зависит только от скорости приёмника света
| |
4)
|
зависит как от скорости приёмника света, так и от скорости источника
света
|
Решение. Согласно постулату
специальной теории относительности скорость света во всех инерциальных
системах отсчёта одинакова и не зависит ни от скорости приёмника света,
ни от скорости источника света.
Правильный ответ: 1.
А23. Бета-излучение — это
|
1)
|
поток ядер гелия
| |
2)
|
поток протонов
| |
3)
|
поток электронов
| |
4)
|
электромагнитные волны
|
Решение.
Бета-излучение
— это поток электронов.
Правильный ответ: 3.
А24. Реакция термоядерного синтеза 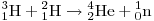 идёт с выделением
энергии, при этом: идёт с выделением
энергии, при этом:
А. Сумма зарядов частиц —
продуктов реакции — точно равна сумме зарядов исходных ядер.
Б. Сумма масс частиц —
продуктов реакции — точно равна сумме масс исходных ядер.
Верны ли приведенные выше утверждения?
|
1)
|
верно только А
| |
2)
|
верно только Б
| |
3)
|
верны и А, и Б
| |
4)
|
не верны ни А, ни Б
|
Решение. Заряд сохраняется
всегда. Поскольку реакция идёт с выделением энергии, суммарная масса
продуктов реакции меньше суммарной массы исходных ядер. Верно только А.
Правильный ответ: 1.
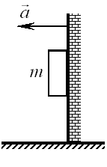 A25. К подвижной вертикальной стенке приложили груз массой
10 кг. Коэффициент трения между грузом и стенкой равен 0,4. С
каким минимальным ускорением надо передвигать стенку влево, чтобы груз
не соскользнул вниз? A25. К подвижной вертикальной стенке приложили груз массой
10 кг. Коэффициент трения между грузом и стенкой равен 0,4. С
каким минимальным ускорением надо передвигать стенку влево, чтобы груз
не соскользнул вниз?
Решение. Чтобы груз не
соскользнул вниз, нужно чтобы сила трения между грузом и стенкой
уравновесила силу тяжести:  . Для неподвижного
относительно стенки груза верно соотношение . Для неподвижного
относительно стенки груза верно соотношение 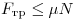 ,
где μ — коэффициент трения, N — сила
реакции опоры, которая по второму закону Ньютона связана с ускорением
стенки равенством ,
где μ — коэффициент трения, N — сила
реакции опоры, которая по второму закону Ньютона связана с ускорением
стенки равенством 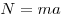 . В итоге получаем: . В итоге получаем:
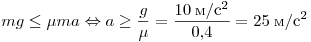 . .
Правильный ответ: 3.
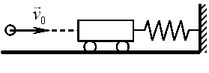 A26.
Пластилиновый шар массой 0,1 кг летит
горизонтально со скоростью 1 м/с (см. рис.). Он налетает на
неподвижную тележку массой 0,1 кг, прикрепленную к легкой пружине,
и прилипает к тележке. Чему равна максимальная кинетическая энергия
системы при её дальнейших колебаниях? Трением пренебречь. Удар считать
мгновенным. A26.
Пластилиновый шар массой 0,1 кг летит
горизонтально со скоростью 1 м/с (см. рис.). Он налетает на
неподвижную тележку массой 0,1 кг, прикрепленную к легкой пружине,
и прилипает к тележке. Чему равна максимальная кинетическая энергия
системы при её дальнейших колебаниях? Трением пренебречь. Удар считать
мгновенным.
|
1)
|
0,1 Дж
| |
2)
|
0,5 Дж
| |
3)
|
0,05 Дж
| |
4)
|
0,025 Дж
|
Решение. По закону сохранения импульса скорость тележки с прилипшим пластилиновым шаром равна
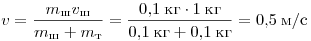 . .
Далее в отсутствии сил трения энергия системы будет
сохраняться. В момент после столкновения потенциальная энергия равна нулю, а кинетическая энергия максимальна:
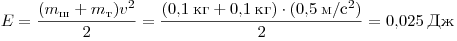 . .
Правильный ответ: 4.
А27. Экспериментаторы закачивают воздух в
стеклянный сосуд,
одновременно охлаждая его. При этом температура воздуха в сосуде
понизилась в 2 раза, а его давление возросло в 3 раза. Во сколько раз
увеличилась масса воздуха в сосуде?
|
1)
|
в 2 раза
| |
2)
|
в 3 раза
| |
3)
|
в 6 раз
| |
4)
|
в 1,5 раза
|
Решение. Используя уравнение Менделеева — Клапейрона, можно рассчитать массу воздуха в сосуде:
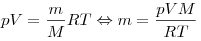 . .
Если температура понизилась в 2 раза, а его давление
возросло в 3
раза, то масса воздуха увеличилась в 6 раз.
Правильный ответ: 3.
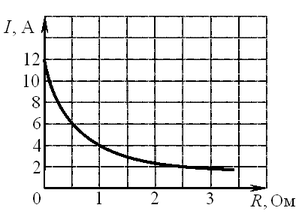 A28. К источнику тока с внутренним сопротивлением 0,5 Ом подключили реостат. На рисунке показан график зависимости силы тока в реостате от его сопротивления. Чему равна ЭДС источника тока? A28. К источнику тока с внутренним сопротивлением 0,5 Ом подключили реостат. На рисунке показан график зависимости силы тока в реостате от его сопротивления. Чему равна ЭДС источника тока?
|
1)
|
12 В
| |
2)
|
6 В
| |
3)
|
4 В
| |
4)
|
2 В
|
Решение. По
закону Ома для
полной цепи:
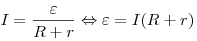 . .
При внешнем сопротивлении равном нуля ЭДС источника тока находится по формуле:
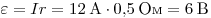 . .
Правильный ответ: 2.
А29. Последовательно соединены конденсатор, катушка
индуктивности и резистор. Если при неизменной частоте и амплитуде
напряжения на концах цепи увеличивать ёмкость конденсатора от 0 до
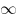 , то амплитуда тока в цепи будет , то амплитуда тока в цепи будет
|
1)
|
монотонно убывать
| |
2)
|
монотонно возрастать
| |
3)
|
сначала возрастать, затем убывать
| |
4)
|
сначала убывать, затем возрастать
|
Решение.
Сопротивление
схемы переменному току равно 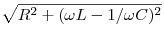 . Амплитуда тока в цепи равна . Амплитуда тока в цепи равна
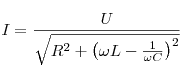 . .
Эта зависимость как функция С на промежутке 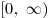 имеет максимум при имеет максимум при 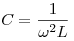 .
Амплитуда тока в цепи будет сначала возрастать, затем убывать. .
Амплитуда тока в цепи будет сначала возрастать, затем убывать.
Правильный ответ: 3.
А30. Сколько α- и β-распадов должно произойти при
радиоактивном распаде ядра урана 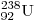 и
конечном превращении его в ядро свинца и
конечном превращении его в ядро свинца 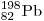 ? ?
|
1)
|
10 α- и 10 β-распадов
| |
2)
|
10 α- и 8 β-распадов
| |
3)
|
8 α- и 10 β-распадов
| |
4)
|
10 α- и 9 β-распадов
|
Решение. При α-распаде
масса ядра уменьшается на 4 а. е. м., а при
β-распаде масса не изменяется. В серии распадов масса ядра
уменьшилась на 238 – 198 = 40 а. е. м. Для
такого уменьшения массы требуется 10 α-распадов. При
α-распаде заряд ядра уменьшается на 2, а при β-распаде
— увеличивается на 1. В серии распадов заряд ядра уменьшился на
10. Для такого уменьшения заряда кроме 10 α-распадов требуется 10
β-распадов.
Правильный ответ: 1.
Часть B
В1. Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, упал обратно на землю через 2 с в 20 м от места броска. Чему равна минимальная скорость
камня за время полёта?
Решение. За 2 с камень
преодолел 20 м по горизонтали, следовательно, составляющая его
скорости, направленная вдоль горизонта, равна 10 м/с. Скорость
камня минимальна в наивысшей точке полёта. В верхней точке полная
скорость совпадает со своей горизонтальной проекцией и, следовательно,
равна 10 м/с.
Ответ: 10.
В2. Для определения удельной теплоты плавления
льда в сосуд с водой стали бросать кусочки тающего льда при непрерывном помешивании. Первоначально в сосуде находилось 300 г воды при температуре
20 °C. К моменту времени, когда лёд перестал таять,
масса воды увеличилась на 84 г. Определите по данным опыта
удельную теплоту плавления льда. Ответ выразите в кДж/кг.
Теплоёмкостью сосуда пренебречь.
Решение. Вода отдала
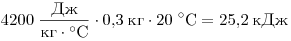 теплоты. Это количество теплоты пошло
на таяние 84 г льда. Удельная теплота плавления льда равна теплоты. Это количество теплоты пошло
на таяние 84 г льда. Удельная теплота плавления льда равна
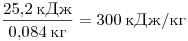 . .
Ответ: 300.
В3. При лечении электростатическим душем к электродам прикладывается разность потенциалов 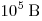 . Какой
заряд проходит между электродами за время процедуры, если известно, что
электрическое поле совершает при этом работу, равную 1800 Дж?
Ответ выразите в мКл. . Какой
заряд проходит между электродами за время процедуры, если известно, что
электрическое поле совершает при этом работу, равную 1800 Дж?
Ответ выразите в мКл.
Решение. Работа электрического поля по перемещению заряда равна 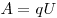 . Откуда можно выразить заряд: . Откуда можно выразить заряд:
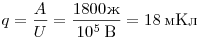 . .
Ответ: 18.
В4. Дифракционная решетка с периодом 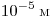 расположена параллельно экрану на расстоянии 1,8 м
от него. Какого порядка максимум в спектре будет наблюдаться на экране
на расстоянии 21 см от центра дифракционной картины при освещении
решетки нормально падающим параллельным пучком света с длиной волны
580 нм? Считать расположена параллельно экрану на расстоянии 1,8 м
от него. Какого порядка максимум в спектре будет наблюдаться на экране
на расстоянии 21 см от центра дифракционной картины при освещении
решетки нормально падающим параллельным пучком света с длиной волны
580 нм? Считать  . .
Решение. Угол отклонения
связан с постоянной решётки и длиной волны света равенством 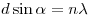 . Отклонение на экране составляет . Отклонение на экране составляет 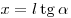 . Таким образом, порядок максимума в спектре равен . Таким образом, порядок максимума в спектре равен
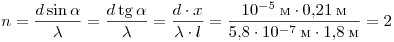 . .
Ответ: 2.
Часть C
С1. Масса Марса составляет 0,1 от массы Земли,
диаметр Марса вдвое меньше, чем диаметр Земли. Каково отношение периодов обращения искусственных спутников Марса и Земли 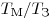 , движущихся по круговым орбитам на небольшой высоте? , движущихся по круговым орбитам на небольшой высоте?
Решение. Период
обращения искусственного спутника, движущегося вокруг планеты по
круговой орбите на небольшой высоте, равен
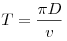 , ,
где D — диаметр планеты, v — скорость
движения спутника, которая связана с центростремительным ускорением
соотношением:
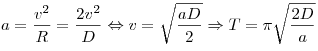 . .
Центростремительное ускорением равно ускорению свободного падения на поверхности планеты (M — масса планеты):
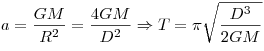 . .
Отношение периодов обращения искусственных спутников
Марса и Земли равно:
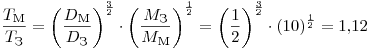 . .
Ответ: 1,12.
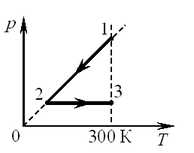 С2. 1 моль идеального одноатомного газа сначала охладили, а затем нагрели до первоначальной температуры 300 К, увеличив объём газа в 3 раза (см. рис.). Какое количество теплоты
отдал газ на участке 1–2? С2. 1 моль идеального одноатомного газа сначала охладили, а затем нагрели до первоначальной температуры 300 К, увеличив объём газа в 3 раза (см. рис.). Какое количество теплоты
отдал газ на участке 1–2?
Решение. Поскольку при изобарном нагревании объём увеличился в 3 раза, температура также увеличилась в 3 раза. Значит, 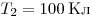 . На участке 1–2 объём газа остаётся постоянным. Теплоёмкость идеального одноатомного газа в изобарном процессе равна . На участке 1–2 объём газа остаётся постоянным. Теплоёмкость идеального одноатомного газа в изобарном процессе равна 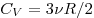 . Количество теплоты, отданное газом на участке 1–2, равно . Количество теплоты, отданное газом на участке 1–2, равно
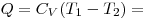
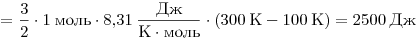 . .
Ответ: 2,5 кДж.
С3. Ученик собрал электрическую цепь, состоящую из батарейки (1), реостата (2), ключа (3), амперметра (4) и вольтметра (5). После этого он провел измерения напряжения на полюсах и силы тока в цепи при двух положениях ползунка реостата (см. рисунки). Определите КПД источника тока в первом опыте.

Решение. Показания
вольтметра равны разности ЭДС и падения напряжения на внутреннем
сопротивлении: 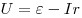 . Из рисунков видно, что
при силе тока в цепи . Из рисунков видно, что
при силе тока в цепи 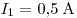 вольтметр показывает напряжение
вольтметр показывает напряжение 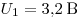 , а при силе тока , а при силе тока 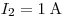 напряжение напряжение 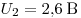 . Т. о. получаем систему двух
уравнений, из которой находим ЭДС батарейки: . Т. о. получаем систему двух
уравнений, из которой находим ЭДС батарейки:
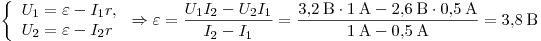 . .
КПД источника тока в первом опыте равен 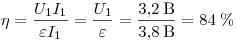 . .
Ответ: 84 %.
С4. На экране с помощью тонкой линзы получено изображение предмета с пятикратным увеличением. Экран передвинули на 30 см
вдоль главной оптической оси линзы. Затем при неизменном положении
линзы передвинули предмет, чтобы изображение снова стало резким. В этом
случае получилось изображение с трёхкратным увеличением. На каком
расстоянии от линзы находилось изображение предмета в первом случае?
Решение. Обозначим
расстояние от линзы до изображения предмета в первом случае x,
фокусное расстояние линзы — f.
Поскольку увеличение в первом
опыте было пятикратным, предмет находился на расстоянии 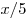 от линзы. Используя формулу для линзы, получаем:
от линзы. Используя формулу для линзы, получаем:
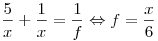 . .
После сдвига экрана, он стал находиться на расстоянии
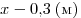 от линзы, а предмет — на расстоянии от линзы, а предмет — на расстоянии 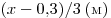 . Вновь используя формулу для линзы, получаем: . Вновь используя формулу для линзы, получаем:
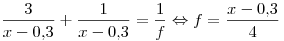 , ,
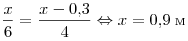 . .
Ответ: 0,9 м.
С5. Какова максимальная скорость электронов, выбиваемых из металлической пластины светом с длиной волны 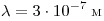 , если красная граница фотоэффекта , если красная граница фотоэффекта 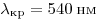 ? ?
Решение. Используя
уравнение Эйнштейна для фотоэффекта, получаем:
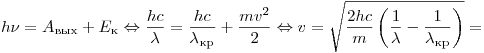
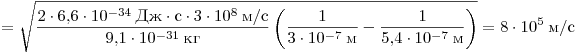 . .
Ответ: 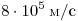 . .
С6. Две параллельные неподвижные диэлектрические пластины расположены вертикально и заряжены разноименно. Пластины находятся на расстоянии d = 2 см друг от друга. Напряжённость
поля в пространстве внутри пластин равна 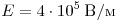 . Между пластинами на равном расстоянии от них помещен
шарик с зарядом . Между пластинами на равном расстоянии от них помещен
шарик с зарядом 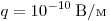 и массой
m = 20 мг. После того как шарик отпустили, он
начинает падать и ударяется об одну из пластин. Насколько уменьшится
высота местонахождения шарика Δh к моменту его удара об
одну из пластин? и массой
m = 20 мг. После того как шарик отпустили, он
начинает падать и ударяется об одну из пластин. Насколько уменьшится
высота местонахождения шарика Δh к моменту его удара об
одну из пластин?
Решение. В
горизонтальном направлении на шарик действует сила 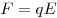 ,
которая сообщает ему ускорение ,
которая сообщает ему ускорение 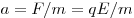 . Для
преодоления по горизонтали расстояния . Для
преодоления по горизонтали расстояния 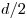 шарику потребуется
время шарику потребуется
время 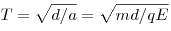 . За это время шарик
сместится вниз на высоту . За это время шарик
сместится вниз на высоту
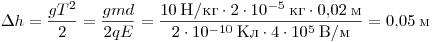 . .
Ответ: 0,05 м.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
| 
