Санкт-Петербургский Государственный Унивеситет
Математико-механический факультет
1977 год
В зависимости от
 указать те указать те  , для которых уравнение , для которых уравнение 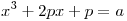 имеет три различных корня. имеет три различных корня.
Найти все решения
уравнения 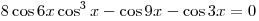 , лежащие
в интервале , лежащие
в интервале 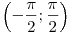 . .
Сколькими способами можно
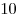 одинаковых подарков распределить между одинаковых подарков распределить между 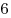 детьми так, чтобы каждый ребенок получил хотя бы один подарок?
детьми так, чтобы каждый ребенок получил хотя бы один подарок?
Определить высоту конуса,
вписанного в шар радиуса 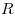 и имеющего наибольшую площадь
полной поверхности. и имеющего наибольшую площадь
полной поверхности.
Вектор
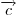 , перпендикулярный векторам , перпендикулярный векторам
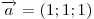 и и 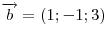 , образует с осью , образует с осью 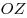 тупой угол. Зная, что тупой угол. Зная, что
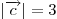 , найти его
координаты. , найти его
координаты.
Ответы
1997 год
При каких значениях параметра
 существует такое значение параметра существует такое значение параметра 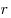 , что
система , что
система 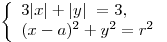 имеет ровно три решения? имеет ровно три решения?
Решите неравенство
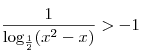 . .
Решите уравнение 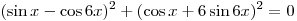 . .
Решите уравнение 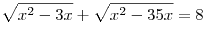 . .
Дана правильная треугольная
пирамида SABC со стороной основания 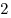 и боковым
ребром и боковым
ребром 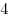 . Найдите объем фигуры, состоящей из всех тех точек
пирамиды, для которых расстояние до вершины . Найдите объем фигуры, состоящей из всех тех точек
пирамиды, для которых расстояние до вершины  не больше
расстояния до любой из вершин основания. не больше
расстояния до любой из вершин основания.
Ответы
2007 год
Две вершины квадрата лежат на
оси абсцисс координатной плоскости 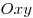 , а две
другие — на графике функции , а две
другие — на графике функции 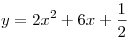 . Найти площадь квадрата. . Найти площадь квадрата.
Решить уравнение 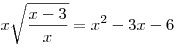 . .
Решить неравенство 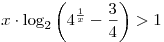 . .
Все вершины правильной
четырёхугольной призмы лежат на поверхности тетраэдра 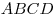 ,
рёбра которого равны ,
рёбра которого равны 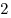 . При этом . При этом  и и
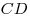 параллельны рёбрам основания призмы. Найти высоту призмы,
если известно, что она в два раза короче каждого из рёбер основания
призмы. параллельны рёбрам основания призмы. Найти высоту призмы,
если известно, что она в два раза короче каждого из рёбер основания
призмы.
Найти все целые положительные
 , при которых уравнение , при которых уравнение 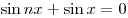 имеет только одно решение на промежутке
имеет только одно решение на промежутке 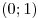 . .
Ответы
Ответы
1977 год
- a) Если
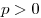 , то , то 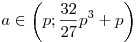 , ,
б) Если 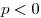 , то , то 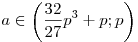 , ,
в) Если 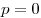 , то решений нет. , то решений нет.
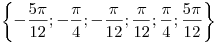 . .
-
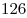 способов.
способов.
- Ответ:
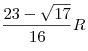 . .
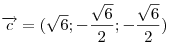 . .
1997 год
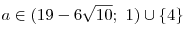 . .
 . .
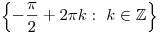 . .
-
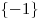 . .
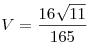 . .
2007 год
- Площадь квадрата равна
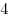 или или 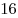 . .
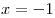 , , 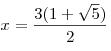 . .
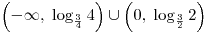 . .
- Высота призмы равна
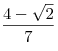 . .
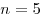 . .
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

