Московский государственный университет им. М.В. Ломоносова
Геологический факультет
1977 год
В бак может поступать
вода через одну из двух труб. Через первую трубу бак можно наполнить на
час быстрее, чем через вторую трубу. Если бы емкость бака была больше
на 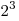 , а пропускная способность второй трубы была бы
больше на , а пропускная способность второй трубы была бы
больше на 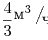 , то для наполнения бака через вторую
трубу понадобилось бы столько же времени, сколько требуется для
пропуска , то для наполнения бака через вторую
трубу понадобилось бы столько же времени, сколько требуется для
пропуска 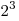 воды через первую трубу. Какова емкость бака,
если известно, что за время его наполнения через вторую трубу через
первую трубу могло бы поступить воды через первую трубу. Какова емкость бака,
если известно, что за время его наполнения через вторую трубу через
первую трубу могло бы поступить 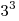 воды? воды?
Решить неравенство
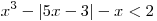 . .
Решить уравнение
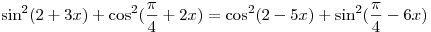 . .
В окружность с центром
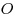 вписан треугольник вписан треугольник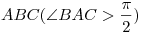 . Продолжение биссектрисы . Продолжение биссектрисы 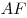 угла угла
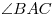 этого треугольника пересекает окружность в точке этого треугольника пересекает окружность в точке
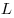 , а радиус , а радиус 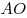 пересекает сторону пересекает сторону  в
точке в
точке 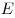 . Пусть . Пусть 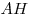 — высота
треугольника — высота
треугольника  . Найти отношение площади треугольника . Найти отношение площади треугольника
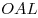 к площади четырехугольника к площади четырехугольника 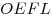 . .
Найти все значения
параметра 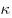 , при каждом из которых существует хотя бы
одно общее решение у неравенств , при каждом из которых существует хотя бы
одно общее решение у неравенств 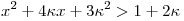 и и 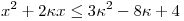 . .
Ответы
1997 год
Решить уравнение ![\frac{{x^3 - x^2 - 6x}}{{\sqrt[5]{x}}} =
0 \frac{{x^3 - x^2 - 6x}}{{\sqrt[5]{x}}} =
0](/inc/pictures/dcff565bbcb0f44cbd5f02eeeb809259.png) . .
Решить уравнение 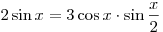 . .
Решить неравенство 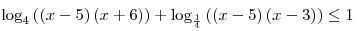 . .
В треугольнике  известны: известны: 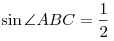 и и 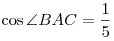 . Найти
отношение длин высот, опущенных соответственно из вершины . Найти
отношение длин высот, опущенных соответственно из вершины  на сторону
на сторону и из вершины и из вершины  на сторону на сторону
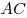 . .
Решить систему уравнений
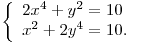
Любой из трех грузовиков разной грузоподъемности при полной загрузке в
каждой поездке может перевести некоторый груз, причем грузовик с
наименьшей грузоподъемностью - за 10 поездок. Сколько совместных
поездок необходимо двум другим грузовикам для перевозки всего груза
(недогрузка запрещается)?
Ответы
2007 год
Решите неравенство 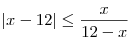 . .
Ответ: ![\left[ {9,16} \right] \left[ {9,16} \right]](/inc/pictures/2b194c3792f9b4f344d0a6d45d8ecb41.png) . .
Решите уравнение 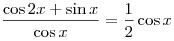 . .
Ответ: 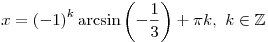 . .
Решите неравенство 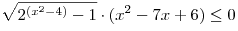 . .
Ответ: ![\left[ {2,6} \right] \left[ {2,6} \right]](/inc/pictures/e35f1a15faed2a8f15df69fa98108fdb.png)
Площадь четырехугольника 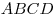 равна 9, радиус вписанной в
него окружности равен 1, а длины сторон равна 9, радиус вписанной в
него окружности равен 1, а длины сторон  и и  равны 3 и 5 соответственно. Чему равны длины сторон
равны 3 и 5 соответственно. Чему равны длины сторон 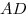 и и
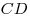 ? ?
Ответ: 6, 4.
Решите неравенство 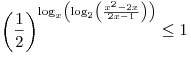 . .
Ответ: 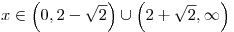 . .
Сумма первых пятнадцати членов арифметической прогрессии, состоящей из
натуральных чисел, больше 337, но меньше 393. Чему равен восьмой член
этой прогрессии, если известно, что он кратен четырем?
Ответ: 24.
Ответы
Ответы
1977 год
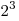 . .
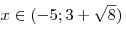 . .
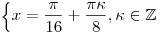 , , 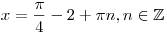 , ,
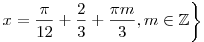 . .
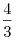 . .
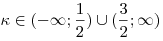 . .
1997 год
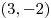 . .
-
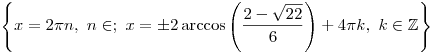 . .
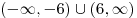 . .
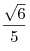 . .
-
- от 1 до 4.
2007 год
![\left[ {9,16} \right] \left[ {9,16} \right]](/inc/pictures/2b194c3792f9b4f344d0a6d45d8ecb41.png) . .
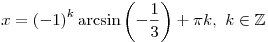 . .
-
![\left[ {2,6} \right] \left[ {2,6} \right]](/inc/pictures/e35f1a15faed2a8f15df69fa98108fdb.png) . .
- 6, 4.
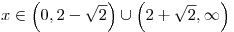 . .
- 24.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

