|
МЕЖДУНАРОДНАЯ ДИСТАНЦИОННАЯ МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА «ТРЕТЬЕ ТЫСЯЧЕЛЕТИЕ»
2009 год
Задачи для 5 класса
Расставьте в клетках квадрата 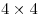 одну единицу, две двойки, одну единицу, две двойки, 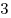 тройки, тройки, 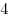 четверки, четверки, 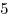 пятерок и еще одну любую цифру по своему выбору так, чтобы во всех строках получилась одна и та же сумма цифр. пятерок и еще одну любую цифру по своему выбору так, чтобы во всех строках получилась одна и та же сумма цифр.
Расположите на плоскости 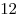 спичек так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов. спичек так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов.
Аня хочет положить в каждую коробку одинаковое число своих игрушек. Сначала она попыталась разложить их по 12 в каждую коробку, но 5 игрушек оказались лишними. Затем она попробовала разложить их по 15 в каждую коробку, но для последней коробки остались только 2 игрушки. Тогда Аня догадалась взять еще одну коробку. Сколько игрушек Аня должна теперь положить в каждую коробку, чтобы добиться своей цели?
Какой цифрой заканчивается десятичная запись числа 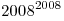 ? ?
Можно ли так расположить на плоскости 5 отрезков, чтобы каждый из них пересекался со всеми остальными, кроме какого-то одного?
Серия трамвайных билетов включает все шестизначные номера от 000000 до 999999. Петербурженка Ася коллекционирует билеты, номера которых делятся на 78. Москвич Вася предпочитает билеты, номера которых делятся на 77, но не делятся на 78. Каких билетов в серии больше и на сколько: интересных Асе или Васе?
Решения задач для 5 класса
Задача 1. Сумма чисел в каждой строке должна равняться 16.
| 5 |
4 |
3 |
4 |
| 5 |
4 |
2 |
5 |
| 1 |
3 |
9 |
3 |
| 5 |
5 |
2 |
4 |
Задача 2. ____________ — размер спички.
25 квадратов 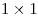 ; ;
16 квадратов 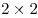 ; ;
9 квадратов 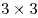 ; ;
4 квадрата 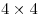 ; ;
1 квадрат 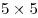 . .
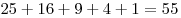 . .
Ответ: 55 квадратов.
Задача 3.
Пусть  — количество тугриков у Васи. Тогда, — количество тугриков у Васи. Тогда, 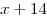 — стоимость 39 солдатиков; — стоимость 39 солдатиков; 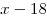 — стоимость 35 солдатиков. Значит, 4 солдатика стоят — стоимость 35 солдатиков. Значит, 4 солдатика стоят 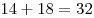 тугрика. 1 солдатик стоит тугрика. 1 солдатик стоит 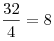 тугриков. У Васи было тугриков. У Васи было 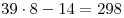 тугриков. тугриков.
Задача 4.

Задача 5.

Единственное решение, когда в феврале 5 пятниц — високосный год и начало месяца в пятницу.
Март — начало в субботу, 31 день, конец — понедельник.
Апрель — начало во вторник, 30 дней, конец — среда.
Май — начало в четверг, 31 день, конец — суббота.
Июнь — начало в воскресенье, 30 дней, конец — понедельник.
Июль — начало во вторник, 31 день, конец — четверг.

Ответ: в июле 5 вторников (високосный год с началом февраля месяца в пятницу).
Задача 6. Макс купил 8 карандашей, это все равно, что 4 авторучки и 4 фломастера, а Петр купил 7 фломастеров. Но 4 авторучки
дороже 3-х фломастеров. Значит, Макс потратил денег больше.
Задачи для 6 класса
Расставьте одну единицу, две двойки, 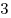 тройки, тройки, 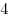 четверки, четверки, 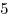 пятерок, пятерок, 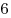 шестерок, шестерок, 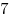 семерок и семерок и 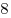 восьмерок в клетках квадрата восьмерок в клетках квадрата 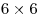 так, чтобы во всех строках была одна и та же сумма цифр. так, чтобы во всех строках была одна и та же сумма цифр.
Расположите на плоскости 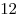 спичек так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов. спичек так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов.
Нарисуйте на клетчатой бумаге квадрат 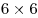 . Проведите через его вершины замкнутую ломаную без самопересечений, все остальные вершины которой тоже лежали бы в узлах сетки, а площадь ограниченной ею фигуры была бы как можно меньше. . Проведите через его вершины замкнутую ломаную без самопересечений, все остальные вершины которой тоже лежали бы в узлах сетки, а площадь ограниченной ею фигуры была бы как можно меньше.
Поверхность большого кубика Рубика состоит из 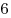 квадратных граней, каждая из которых разбита на квадратных граней, каждая из которых разбита на 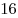 клеток клеток 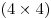 . Муравей может из любой клетки переползти в
любую из четырех соседних – имеющих с ней общую сторону (в
той же грани, либо через ребро). Помогите муравью обойти все клетки,
побывав в каждой из них ровно по одному разу. . Муравей может из любой клетки переползти в
любую из четырех соседних – имеющих с ней общую сторону (в
той же грани, либо через ребро). Помогите муравью обойти все клетки,
побывав в каждой из них ровно по одному разу.
Магазин снизил цену товара в два раза, благодаря чему продал его в 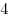 раза больше. Как и во сколько раз изменилась выручка магазина? раза больше. Как и во сколько раз изменилась выручка магазина?
Четыре фломастера стоят дороже пяти авторучек, четыре авторучки дороже трех фломастеров, а два карандаша ровно столько же, сколько фломастер и авторучка вместе взятые. Антон купил 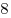 карандашей, а Борис –
карандашей, а Борис – 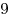 авторучек. Кто из мальчиков потратил больше денег? авторучек. Кто из мальчиков потратил больше денег?
Решения задач для 6 класса
Задача 1.
| 8 |
8 |
7 |
6 |
2 |
3 |
| 5 |
5 |
4 |
6 |
7 |
7 |
| 4 |
8 |
5 |
7 |
7 |
3 |
| 6 |
6 |
4 |
7 |
3 |
8 |
| 8 |
7 |
6 |
8 |
4 |
1 |
| 8 |
8 |
6 |
5 |
5 |
2 |

Задача 2. Вариант №1 трактовки условия задачи.
Если условие задачи «расположите на плоскости 12 спичек» трактовать так, что
спички не должны лежать одна на другой, имеем единственную расстановку
(см. рисунок).
Получили четыре квадрата с длинной
стороны в одну спичку и один квадрат с длинной стороны в две спички,
итого пять квадратов.
Ответ: 5 квадратов.
Вариант №2 трактовки условия задачи.
Если условие задачи «как можно больше различных квадратов» понимать так: различные квадраты — это квадраты с разной длиной стороны, т.е одинаковые квадратики я считаю один раз, то имеем:
1. Из четырех спичек построим квадрат 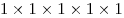

2. Положим по одной спичке по вертикали и горизонтали на одинаковом расстоянии от точки  . .

Получили два новых квадрата.
3. Добавим еще по одной вертикальной и горизонтальной спичке на одинаковом расстоянии от точки  . Получим три новых квадрата. . Получим три новых квадрата.

4. Добавим еще по одной вертикальной и горизонтальной спичке на одинаковом расстоянии от точки  . Получим четыре новых квадрата. . Получим четыре новых квадрата.

5. Добавим еще по одной вертикальной и горизонтальной спичке на одинаковом расстоянии от точки  . Получим пять новых квадратов. . Получим пять новых квадратов.
Итого получили 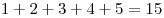 различных квадратов, т.е. все 15 квадратов имеют разную площадь. различных квадратов, т.е. все 15 квадратов имеют разную площадь.
Вариант №3 трактовки условия задачи.
Разложим шесть спичек по вертикали и шесть спичек по горизонтали на одинаковом расстоянии друг от друга, горизонтальный ряд спичек лежит на вертикальном.
Подсчитаем всевозможные получившиеся квадраты, в том числе квадраты одинаковой площади.

Одноклеточных квадратов — 25 шт.;
Четырехклеточных квадратов — 16 шт.;
Девятиклеточных квадратов — 9 шт.;
Шестнадцатиклеточных квадратов — 4 шт.;
Двадцатипятиклеточный квадрат — 1 шт.
Итого: 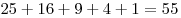 квадратов. квадратов.
Ответ: 55 квадратов.
Задача 3.

Задача 4. Возьмем развертку куба и покажем маршрут муравья. Рассмотрим три случая:
1. Муравей стартует из граничной, но не угловой клетки (эти клетки равнозначны с точностью до поворота кубика);
2. Муравей стартует из одной из четырех центральных клеток (эти клетки равнозначны с точностью до поворота кубика);
3. Муравей стартует из угловой клетки (эти клетки равнозначны с точностью до поворота кубика).
Маршрут: клетка 1 — клетка 2 — клетка 3 — клетка 4.



Задача 5. Пусть  — столько единиц товара продавал магазин до снижения цены в единицу времени; — столько единиц товара продавал магазин до снижения цены в единицу времени;  —
стоимость единицы товара до снижения цены. —
стоимость единицы товара до снижения цены.
Тогда 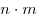 — выручка магазина до снижения цены товара; — выручка магазина до снижения цены товара; 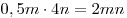 — выручка магазина после снижения цены товара; — выручка магазина после снижения цены товара; 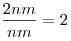 — во столько раз увеличилась выручка магазина после снижения цены товара. — во столько раз увеличилась выручка магазина после снижения цены товара.
Ответ: после снижения цены товара в два раза выручка магазина
увеличилась в два раза.
Задача 6. По условию задачи:
1) 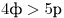 — четыре фломастера стоят дороже пяти авторучек; — четыре фломастера стоят дороже пяти авторучек;
2) 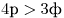 — четыре авторучки стоят дороже трех фломастеров; — четыре авторучки стоят дороже трех фломастеров;
3) 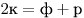 — два карандаша стоят столько, сколько фломастер и ручка вместе взятые; — два карандаша стоят столько, сколько фломастер и ручка вместе взятые;
 — что дороже, 8 карандашей или 9 ручек? — что дороже, 8 карандашей или 9 ручек?
Из (3) имеем:
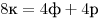 . (4) . (4)
По условию (1) имеем:
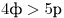 . .
Тогда
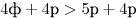 , ,
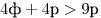 , ,
но по (4) имеем
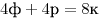 , ,
тогда
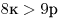 , ,
т.е. восемь карандашей стоят дороже девяти авторучек.
Ответ: Антон, купив восемь карандашей, потратил больше денег, чем Борис, который купил девять авторучек.
Задачи для 7 класса
Расставьте одну единицу, две двойки, 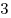 тройки, тройки, 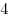 четверки, четверки, 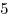 пятерок, пятерок, 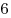 шестерок, шестерок, 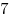 семерок и семерок и 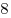 восьмерок в клетках квадрата восьмерок в клетках квадрата 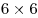 так, чтобы во всех строках была одна и та же сумма цифр. так, чтобы во всех строках была одна и та же сумма цифр.
Расположите на плоскости 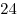 спички так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов. спички так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов.
Найдите все пары натуральных чисел  и и  , для которых , для которых 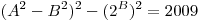 . .
Поверхность гигантского кубика Рубика состоит из 6 квадратных граней, каждая из которых разбита на 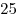 клеток клеток 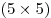 . Муравей может из любой клетки переползти в любую из
четырех соседних – имеющих с ней общую сторону (в той же
грани, либо через ребро). Помогите муравью обойти все клетки, побывав в
каждой из них ровно по одному разу. . Муравей может из любой клетки переползти в любую из
четырех соседних – имеющих с ней общую сторону (в той же
грани, либо через ребро). Помогите муравью обойти все клетки, побывав в
каждой из них ровно по одному разу.
Магазин снизил цену товара на 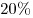 , благодаря чему продал его на , благодаря чему продал его на 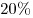 больше. На сколько процентов и в какую сторону изменилась выручка магазина? больше. На сколько процентов и в какую сторону изменилась выручка магазина?
Восемь фломастеров стоят дороже четырех карандашей и пяти авторучек, четыре авторучки дороже трех фломастеров, а два карандаша ровно столько же, сколько фломастер и авторучка вместе взятые. Юрий купил
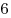 фломастеров, а Павел – фломастеров, а Павел – 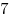 авторучек. Кто из мальчиков потратил больше денег? авторучек. Кто из мальчиков потратил больше денег?
Решения задач для 7 класса
Задача 1.
| 8 |
7 |
6 |
5 |
5 |
3 |
| 8 |
7 |
8 |
7 |
4 |
2 |
| 8 |
7 |
6 |
8 |
3 |
2 |
| 8 |
7 |
6 |
8 |
4 |
1 |
| 8 |
7 |
6 |
3 |
4 |
4 |
| 8 |
7 |
6 |
5 |
5 |
3 |
Ответ: в каждой строке сумма цифр равна 34.
Задача 2. В случае, когда спички нельзя накладывать одну на одну, ответ — 14:
А в случае, когда можно накладывать спички одну на одну, ответ — 506:
Здесь получается: по 11 квадратов 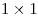 в строке и в столбце, по 10 квадратов в строке и в столбце, по 10 квадратов 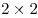 в строке и в столбце, по 9 квадратов в строке и в столбце, по 9 квадратов 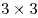 в строке и в столбце, по 8 квадратов в строке и в столбце, по 8 квадратов 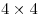 в строке и в столбце, по 7 квадратов в строке и в столбце, по 7 квадратов 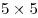 в строке и в столбце, по 6 квадратов в строке и в столбце, по 6 квадратов 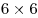 в строке и в столбце, по 5 квадрата в строке и в столбце, по 5 квадрата 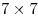 в строке и в столбце и 4 квадрата в строке и в столбце и 4 квадрата 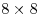 , по 3 квадрата , по 3 квадрата 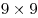 в строке и столбце, по 2 квадрата в строке и столбце, по 2 квадрата 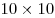 в строке и столбце, и 1 квадрат в строке и столбце, и 1 квадрат 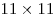 . .
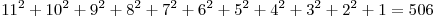 . .
Задача 3.
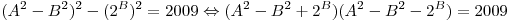 . .
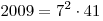 , из этого следует, что у числа 2009 6 делителей: 1, 2009, 7, 41, 287, 49, которые мы можем разбить на пары: 1, 2009; 7, 287; 41, 49. , из этого следует, что у числа 2009 6 делителей: 1, 2009, 7, 41, 287, 49, которые мы можем разбить на пары: 1, 2009; 7, 287; 41, 49.
Так как 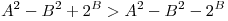 , то , то 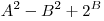 всегда будет равняться большему числу. всегда будет равняться большему числу.
1)
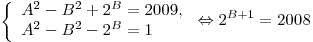 . .
Но такое не возможно, потому что 2008 не является степенью двойки.
2)
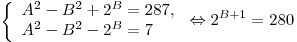 . .
А это также невозможно т.к. 280 не является степенью двойки.
3)
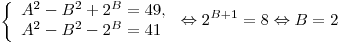 . .
Теперь подставляем  в первое уравнение: в первое уравнение:
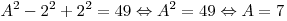 . .
Но так же эти два уравнения могут равняться и отрицательным числам: 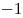 , , 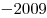 ; ; 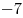 , , 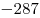 ; ; 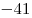 , , 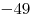 . .
4)
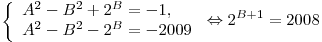 . .
Но это не возможно по аналогии со случаем №1.
5)
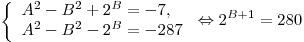 . .
Такого быть также не может, аналогично случаю №2.
6)
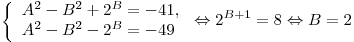 . .
Теперь подставляем 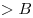 в первое уравнение: в первое уравнение:
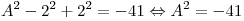 , ,
что также невозможно потому, что 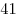 — не степень цифры два. — не степень цифры два.
Ответ: 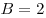 , , 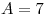 . .
Задачи для 8 класса
Расставьте одну единицу, две двойки, 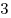 тройки, тройки, 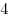 четверки, четверки, 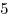 пятерок, пятерок, 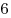 шестерок, шестерок, 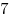 семерок и семерок и 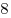 восьмерок в клетках квадрата восьмерок в клетках квадрата 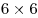 так, чтобы во всех строках была одна и та же сумма цифр. так, чтобы во всех строках была одна и та же сумма цифр.
Расположите на плоскости 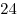 спички так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов. спички так, чтобы они образовали как можно больше различных квадратов. Укажите в ответе число этих квадратов.
Найдите все пары натуральных чисел  и и  , для которых , для которых 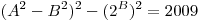 . .
У двух различных треугольников попарно равны все углы и две пары сторон. Длины этих сторон (из разных пар) относятся друг к другу как 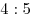 . Найдите отношение площадей этих треугольников. . Найдите отношение площадей этих треугольников.
Однажды в феврале было пять пятниц. В каких месяцах того же года было по пять воскресений?
Два карандаша стоят ровно столько же, сколько фломастер и авторучка вместе взятые, а 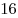 фломастеров стоят дороже девяти карандашей и десяти авторучек (вместе взятых). Кирилл купил фломастеров стоят дороже девяти карандашей и десяти авторучек (вместе взятых). Кирилл купил
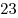 фломастера, а Михаил – фломастера, а Михаил – 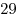 авторучек. Кто из мальчиков потратил больше денег? авторучек. Кто из мальчиков потратил больше денег?
Задачи для 9 класса
Расставьте 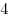 четверки, четверки, 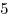 пятерок, пятерок, 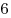 шестерок, шестерок, 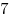 семерок, семерок, 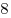 восьмерок, восьмерок, 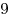 девяток и девяток и 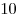 троек в клетках квадрата троек в клетках квадрата 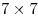 так, чтобы во всех строках была одна и та же сумма цифр. так, чтобы во всех строках была одна и та же сумма цифр.
Даны две концентрические окружности. В большей из них провели хорду, которая оказалась касательной для меньшей окружности. Найдите площадь кольца между окружностями, зная, что длина этой хорды равна 9.
Найдите все пары натуральных чисел  и и  , для которых , для которых 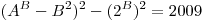 . .
У двух различных треугольников попарно равны все углы и две пары сторон. Длины этих сторон (из разных пар) относятся друг к другу как 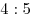 . Найдите отношение площадей этих треугольников. . Найдите отношение площадей этих треугольников.
Найдите все натуральные числа, равные сумме квадратов своих цифр.
Нарисуйте на клетчатой бумаге квадрат 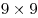 . Проведите через его вершины замкнутую ломаную без самопересечений, все остальные вершины которой тоже лежали бы в узлах сетки, а площадь ограниченной ею фигуры была бы как можно меньше. . Проведите через его вершины замкнутую ломаную без самопересечений, все остальные вершины которой тоже лежали бы в узлах сетки, а площадь ограниченной ею фигуры была бы как можно меньше.
Задачи для 10 класса
Расставьте 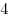 четверки, четверки, 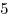 пятерок, пятерок, 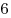 шестерок, шестерок, 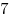 семерок, семерок, 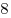 восьмерок, восьмерок, 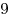 девяток и девяток и 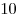 троек в клетках квадрата троек в клетках квадрата 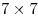 так, чтобы во всех строках была одна и та же сумма цифр. так, чтобы во всех строках была одна и та же сумма цифр.
Даны две концентрические окружности. В большей из них провели хорду, которая оказалась касательной для меньшей окружности. Найдите площадь кольца между окружностями, зная, что длина этой хорды равна 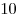 . .
Найдите все натуральные  , для которых , для которых 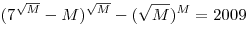 . .
Кратчайшей между двумя точками на поверхности куба называется ломаная наименьшей длины с концами в этих точках, целиком лежащая на поверхности куба (в случае точек из одной грани это будет отрезок). Треугольником на поверхности куба называют наименьшую по площади
область на поверхности куба, границей которой служат кратчайшие, попарно соединяющие три точки. Какое наибольшее число вершин куба может оказаться внутри треугольника на его поверхности?
Найдите все натуральные числа, равные сумме квадратов своих цифр.
Окружность радиуса 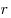 с центром в точке с центром в точке 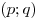 на координатной плоскости пересекает параболу на координатной плоскости пересекает параболу 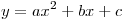 в четырех различных точках. Докажите, что через те же в четырех различных точках. Докажите, что через те же
 точки проходит еще одна парабола. Составьте её уравнение. точки проходит еще одна парабола. Составьте её уравнение.
Задачи для 11 класса
Расставьте 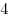 четверки, четверки, 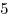 пятерок, пятерок, 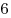 шестерок, шестерок, 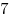 семерок, семерок, 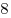 восьмерок, восьмерок, 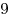 девяток и девяток и 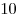 троек в клетках квадрата троек в клетках квадрата 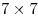 так, чтобы во всех строках была одна и та же сумма цифр. так, чтобы во всех строках была одна и та же сумма цифр.
Даны две концентрические окружности. В большей из них провели хорду, которая оказалась касательной для меньшей окружности. Найдите площадь кольца между окружностями, зная, что длина этой хорды равна 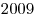 . .
Найдите все натуральные  , для которых , для которых 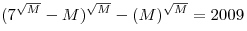 . .
Кратчайшей между двумя точками на поверхности куба называется ломаная наименьшей длины с концами в этих точках, целиком лежащая на поверхности куба (в случае точек из одной грани это будет отрезок). Треугольником на поверхности куба называют наименьшую по площади
область на поверхности куба, границей которой служат кратчайшие, попарно соединяющие три точки. Какую наибольшую площадь может иметь треугольник на поверхности куба с ребром длины 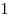 ? ?
Приведите пример двух функций 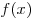 и и 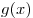 , одна из которых монотонно возрастает, а другая монотонно убывает, для которых равенство , одна из которых монотонно возрастает, а другая монотонно убывает, для которых равенство 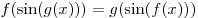 имеет смысл и выполняется при любом вещественном имеет смысл и выполняется при любом вещественном  . .
Производные многочленов 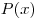 и и 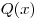 нацело делятся на нацело делятся на 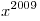 . Докажите, что таким же свойством обладает и их произведение. . Докажите, что таким же свойством обладает и их произведение.
 Оставить комментарий Оставить комментарий
 Сообщить об ошибке Сообщить об ошибке
|

